ABSTRACT
Calibration laboratories routinely participate in interlaboratory comparisons (ILCs), also referred to as Proficiency Testing (PT), in which their measurement of an item should agree with the best estimate of its “actual” or “true” value within pre-established criteria. The PT provider (or participants) must decide how to estimate this “assigned value”, or “Reference Value” (RV), as well as its uncertainty, U(RV), before performing the ILC. Obtaining RV from a superior external (non-participant) laboratory is ideal, but circumstances may require RV to be estimated from participants’ results (consensus value). In the latter case, RV may be estimated from the mean, weighted mean or median of participant results, and, equally importantly, U(RV) may be estimated from prior experience, from participants’ calculated uncertainties or from the spread of participant results. Outliers may affect a consensus value significantly, particularly when there are few participants (small ILC) – robust estimators aim to reduce such effects. This paper discusses approaches to estimating RV and U(RV), for PT in the field of calibration, and particularly for small ILCs. Examples from Thermometry are presented.

INTRODUCTION

Accredited calibration laboratories are required to participate in Proficiency Testing (PT) / interlaboratory comparisons (ILC), to monitor the validity of their results [ILAC-P9:01/2024, “ILAC Policy for Participation in Proficiency Testing Activities”]. This involves measuring an item (for example, the mass of a weight, or the correction of a digital thermometer at certain temperatures) and then comparing the laboratory’s result to the item’s “assigned value” (, also called Reference Value, RV), which should represent the “true” value (traceable to the relevant SI unit(s)), within a particular uncertainty ( or U(RV)). The goal is to demonstrate “equivalence to the SI”, within a certain uncertainty. In practice, this often becomes “equivalence to some reputable laboratories performing such calibrations”, or “equivalence to some other laboratories performing such calibrations”.

In which circumstances would “equivalence to some other laboratories performing such calibrations” constitute evidence of “equivalence to the SI”? If the laboratories use independent measurement standards, equipment, methods and personnel, the chances of their results agreeing (within their uncertainties) while being in error (by more than their uncertainties) should hopefully be small. Note: Laboratories may make similar, large errors and thereby invalidate this argument: examples are – not applying isotopic correction to water triple point temperature [CCT-K7.2002], using inadequate immersion depth for a short thermometer, or using too small a target size for an infrared radiation thermometer. The greater the variety of equipment and methods used, the smaller the chance of such errors affecting all participants equally and thus going unnoticed. Though calibration labs generally use similar, generic calibration methods, differences in, for example, stabilisation time allowed, medium used to compare thermometers (liquid or air bath), or distances used to estimate Size of Source Effect of an infrared thermometer, may cause differences between participant results that allow errors to be identified.
As multiple PT participants within one laboratory usually share the same measurement standards, equipment and method, their results often cluster together more closely than results from different laboratories. For this reason, it adds greatly to the understanding of the result set, if it can be seen which participants are from the same laboratory. This can be done, while maintaining confidentiality, by using participant codes such as “A.1, A.2, A.3″ from laboratory A, “B.1, B.2″ from laboratory B, etc.

In the following sections, the determination of RV and U(RV) using various approaches will be discussed. References to paragraph numbers from ISO 13528:2015 [ISO 13528:2015, “Statistical methods for use in proficiency testing by interlaboratory comparison”] are included for convenience.

7.5 RESULT FROM ONE LABORATORY

The simplest choice of RV is the result of a better laboratory (often a National Metrology Institute, or NMI), not participating in the ILC, that achieves a smaller calibration uncertainty than any participant. Then, U(RV) may be simply the expanded uncertainty reported by this laboratory, with a component for the PT item’s instability during circulation added in quadrature, if such instability is significant. (u_stab is insignificant relative to u_cal if u_stab < 1/3∙u_cal.)
Note: Whether the “superior” laboratory is accredited, or even an NMI, its result may not be flawless, and should be used with care.

7.7 CONSENSUS VALUE FROM PARTICIPANT RESULTS

A superior, non-participant result is not always available. Then, RV must be estimated from participant results (either all participants, or a subset of participants “determined to be reliable, by some pre-defined criteria, such as accreditation status” [13528 clause 7.7.1.1]).
In general, the more participants contributing to RV, the better. However, noting the observation above about clustering of results from one laboratory, it is suggested that the same number of results from each laboratory be included in RV, so as not to bias RV towards the most populous laboratory(ies). In practice, this usually means choosing one result from each laboratory to contribute to RV – this choice may be made by the laboratory itself (before having sight of the full result set).

When there are “few” participants (up to 7, according to EA-4/21 [EA-4/21 INF: 2018, “Guidelines for the assessment of the appropriateness of small interlaboratory comparison within the process of laboratory accreditation”], or fewer than 30, according to the IUPAC/CITAC Guide [IUPAC/CITAC Guide: Selection and use of proficiency testing schemes for a limited number of participants – chemical analytical laboratories (IUPAC Technical Report), Pure Appl. Chem., Vol. 82, No. 5, pp. 1099–1135, 2010]), additional care is required in the choice of RV and U(RV): outliers may be difficult to detect, and inclusion or exclusion of one result may significantly change RV.
For an ILC with few participants, but using a consensus RV, it is suggested that each participant’s result be compared to a Reference Value that excludes its own result. In this way, the participant does not unreasonably bias RV “towards itself”. (In the extreme example of a bilateral comparison, if participant A’s result is (0.00 ± 0.45) and participant B’s result is (1.00 ± 0.45), it is clear that the results do not agree. However, if RV is chosen as the mean of A and B, each participant’s difference from the Reference Value, |LV-RV|, becomes 0.5 and both results pass with |En| < 1!) In other words, for laboratory A, RV should be calculated from the results of laboratories B, C and D (if four participating laboratories), etc. This approach has the drawback that RV is different for each participant, but has the larger benefit that significant bias is removed from RV. (As mentioned in 13528 clause 5.4.1, “a participant could be evaluated against an inappropriate comparison group”.)

a) U(RV) FROM PARTICIPANT UNCERTAINTIES
As a calibration result always includes an estimated uncertainty (which is not the case for many testing results), the uncertainty of a consensus value may be estimated from the uncertainty of each contributing result. If reported uncertainties are considered reliable, the contribution of each result to the average may be weighted by its variance (square of standard uncertainty σ) – the result is the weighted mean, , which would then be RV. The variance of the weighted mean is given by , and U(RV) = . The benefit of this approach is that, if participant uncertainties are reliable, they are taken into account appropriately in forming both RV and U(RV). (The approaches in b), below, do not take estimated uncertainties into account at all, only the spread of results.) The drawback of the weighted mean is that U(RV) does not include any factors arising from instability/drift of the ILC item (which would only become apparent during circulation of the item).

b) U(RV) FROM SPREAD OF PARTICIPANT RESULTS
If participant uncertainties are not reliable, the simple (unweighted) mean may be used as RV, and the Experimental Standard Deviation of the Mean (ESDM), multiplied by Student’s t-factor (to expand to 95% level of confidence while compensating for limited degrees of freedom), used as U(RV).

However, an estimator that is more robust against outliers is the median [13528 clause C.2.1], which is the middle value when participant results are sorted in increasing order. Its standard deviation may be estimated by the scaled median absolute deviation (MADe), which is calculated as follows [13528 clause C.2.2]:

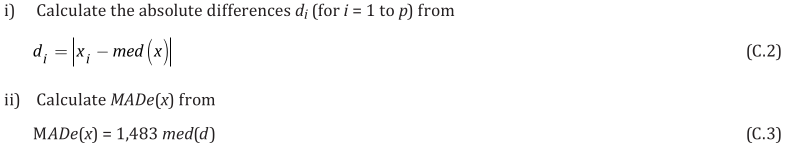
This “robust standard deviation” s* is converted to standard uncertainty of the assigned value, , as follows [13528 clause 7.7.3]:

where p is the number of participants contributing to RV. This may then be expanded to 95% level of confidence by multiplying by Student’s t-factor for degrees of freedom p-1.

EXAMPLE: AN INFRARED THERMOMETRY ILC

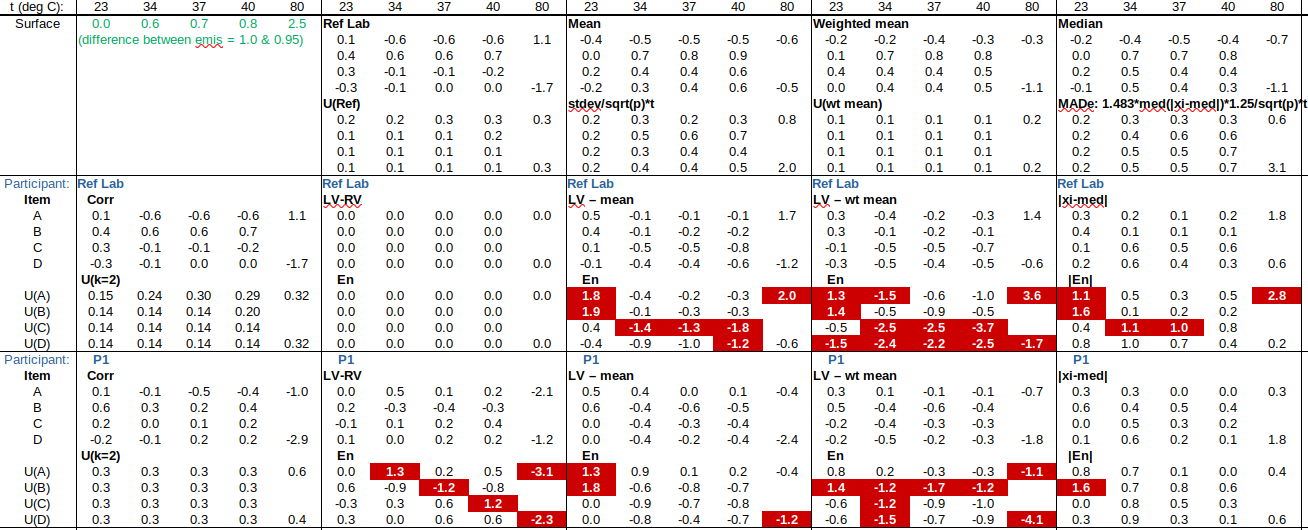
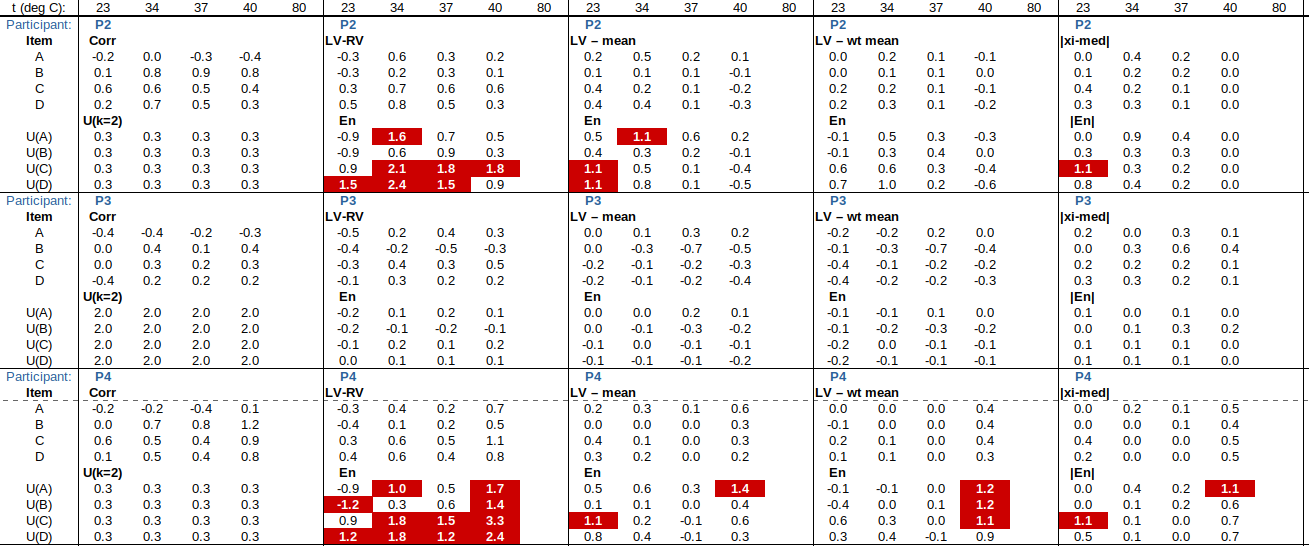
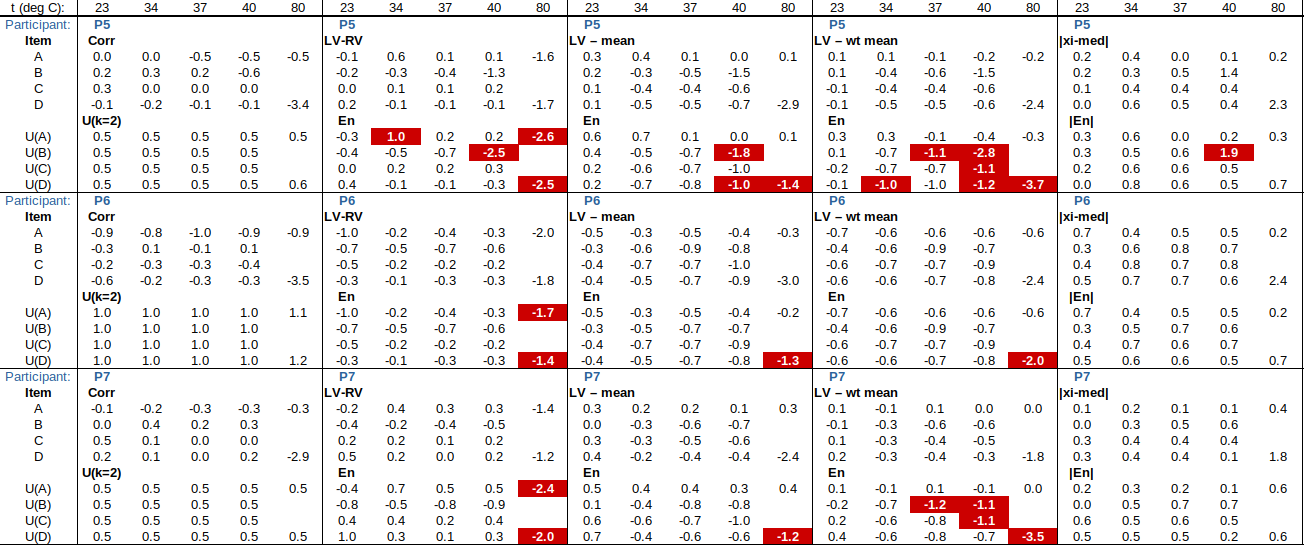
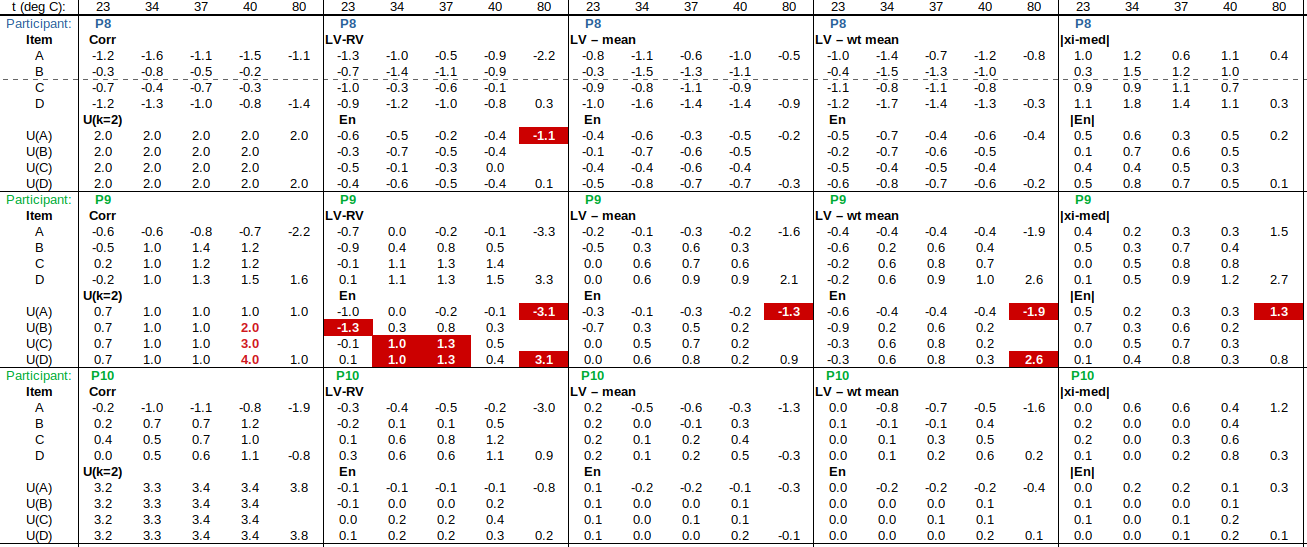
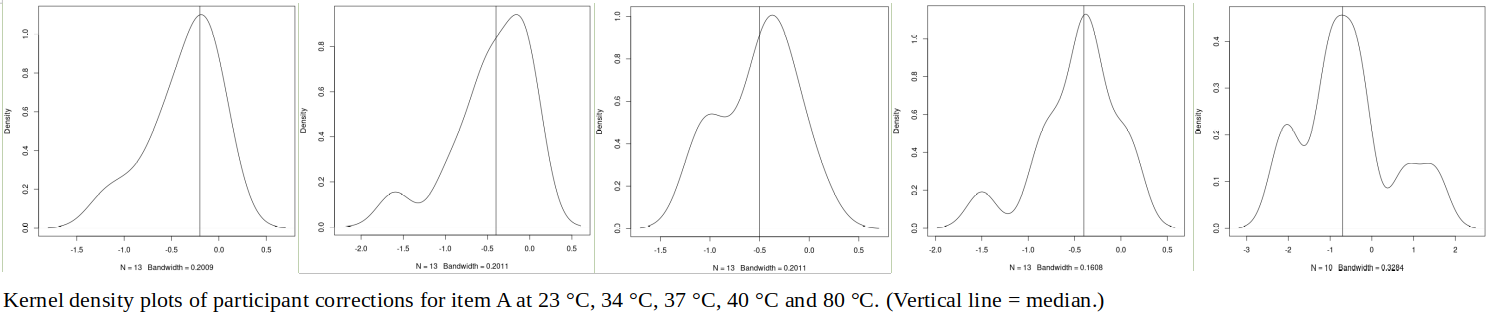
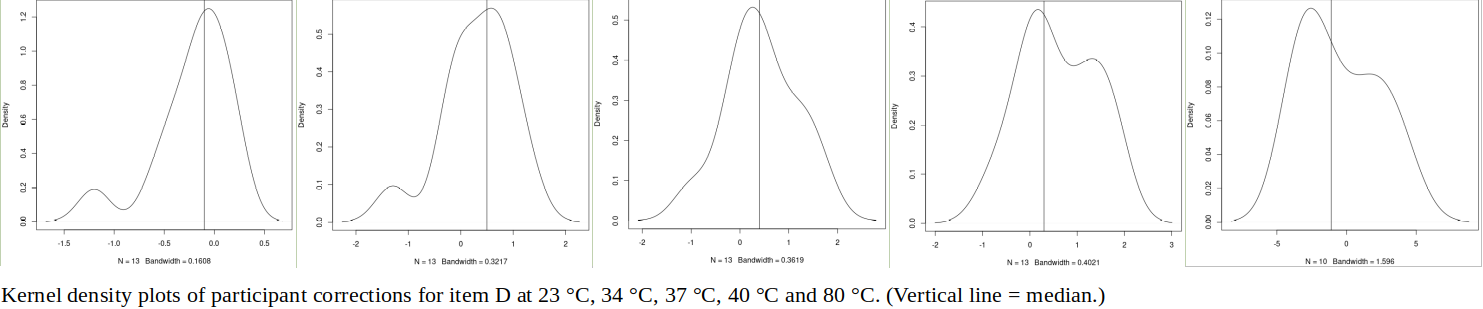
The tables below show corrections for four infrared thermometers (A to D) at five temperatures (from 23 to 80 °C), reported by a superior reference laboratory (Ref Lab) and by 13 ILC participants (P1 to P13). As recommended in 13528 clause 6.4, graphs are presented for visual review of data. (In this case, kernel density plots [13528 clause 10.3] are prepared for items A and D.) Participant results are compared to various assigned values (Ref Lab, mean, weighted mean and median), and participant performance evaluated using En scores [13528 clause 9.7]. The results and choices of RV are discussed below.

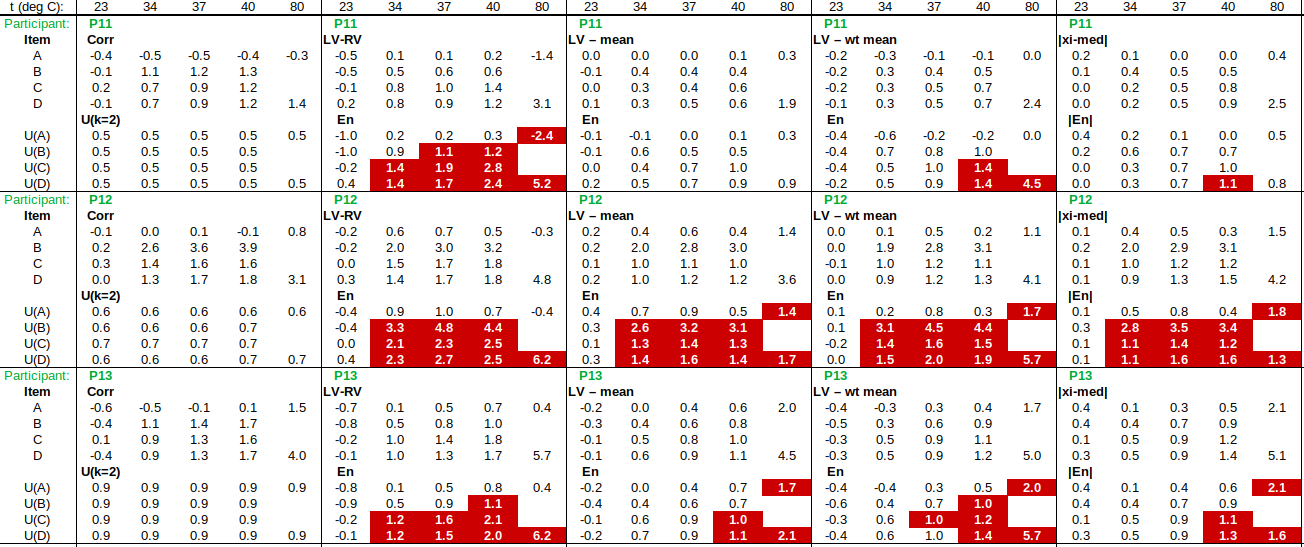
The following observations are made, regarding the above data:
∙The kernel density plots indicate that results at most temperatures are multi-modal and not symmetric, which may cause problems in data analysis, as mentioned in 13528 clause 5.3 (“Most common analysis techniques for proficiency testing assume that a set of results … will be approximately normally distributed, or at least unimodal and reasonably symmetric”). Even robust analysis techniques [13528 Annex C] assume symmetric distribution of data.
∙The spread of participant results, as represented by U(mean) or U(median), is larger than the uncertainties estimated by participants, represented by U(weighted mean), at all temperatures, but the difference is particularly large at 80 °C. This indicates that participants either neglected significant uncertainty components, or that the items drifted significantly during circulation, or both.
∙Some results of Ref Lab, particularly that for item A at 80 °C, are suspect when compared to the median of participant results. As mentioned above, even a reliable reference laboratory should be used with care.

CONCLUSION

∙Obtaining an assigned value for a PT scheme from a superior reference laboratory has the benefit of simplicity, but, as shown in a real-world example, such a Reference Value should still be checked for consistency with a consensus value calculated from participant results [13528 clause 7.8].
∙The use of participant uncertainties to estimate , such as in the weighted mean, may under-represent certain uncertainty contributions, such as drift of the item, but is still useful to demonstrate equivalence of laboratories’ results, which is one of the purposes of Proficiency Testing.
∙Using the spread of participant results to estimate , such as in the scaled median absolute deviation (MADe), captures effects such as drift in the item, but does not incorporate the participants’ own estimates of uncertainty into .
∙Visual review of PT data, for example using kernel density plots, is a convenient way to obtain an overview of what may be a large and complex data set.
∙Two techniques for removing bias from a consensus value are: (i) If there are multiple participants from some laboratories, use only one result from each laboratory to contribute to . (ii) If there are few participants, compare each participant result to a consensus value determined from the other participants’ results, i.e., excluding the participant’s own result.

Contact the author at LMC-Solutions.co.za.