The topic of this article is the determination of the resistance ratio, , of a platinum resistance thermometer (PRT) at a thermometric fixed point, such as the freezing point of zinc (, on the ITS-90 temperature scale). It will discuss the data that should be recorded, the analysis of that data and the estimation of the Uncertainty of Measurement (UoM).

The design of fixed point cells and procedures to realise the required phase transitions are described elsewhere (for example, in Supplementary Information for the ITS-90, also called “the Red Book”). Likewise, using values of at several temperatures , together with their uncertainties, , to calculate ITS-90 deviation function coefficients and propagate uncertainty, is covered in papers such as MSL Technical Guide 21 – Using SPRT Calibration Certificates. Here, we only discuss data needed to determine and to estimate for one fixed point temperature.

The quantity to be determined is resistance ratio: this is the ratio of the PRT’s resistance at the fixed point temperature , , to that at the triple point of water (0.01 °C), .

Often, more than one PRT will be measured during the melt and freeze plateaus. One PRT must be measured repeatedly, to evaluate certain uncertainty components. We will call this “PRT1″, and the others, “additional PRTs”.

DATA TO BE RECORDED:

1. For each PRT, and the measurement at the fixed point.

Notes:

a) All three of the resistances, , and , should be measured using the same resistance measuring instrument, on the same range. If it is a bridge, the same standard resistor should be used, too. This is so that two uncertainty components, calibration uncertainty of the standard resistor, and errors in range amplifiers or attenuators, cancel out in the ratio, and only non-linearity of the measuring instrument remains.

b) If a bridge is used with the same standard resistor, bridge ratios may be recorded in place of resistances. Since the standard resistor value, , is constant (except for its temperature variation, considered in the uncertainty analysis, later), using , or just , will give the same resistance ratio. This applies for all resistance records mentioned below, except when noted otherwise.

c) Don’t confuse “bridge ratio”, , and “resistance ratio”, .

2. Furnace or bath setpoints used for melt, supercool, and freeze. This is so that we can change these setpoint temperatures next time, to achieve longer plateaus. Note: Do not make the setpoints so close to the fixed point temperature that stable furnace control may be mistaken for a plateau. Also, ensure that temperature variation does not take the furnace below the melting temperature at certain points during the control cycle (during the melt), or above the freezing temperature (during the freeze). Rather sacrifice some plateau time, and get unambiguous plateaus.

3. Melt:

(Note: The y-axes of the graphs below are graduated in temperature units, for convenient visual interpretation. Readings could, equivalently, have been plotted as resistance ratios , resistances , or bridge ratios.)

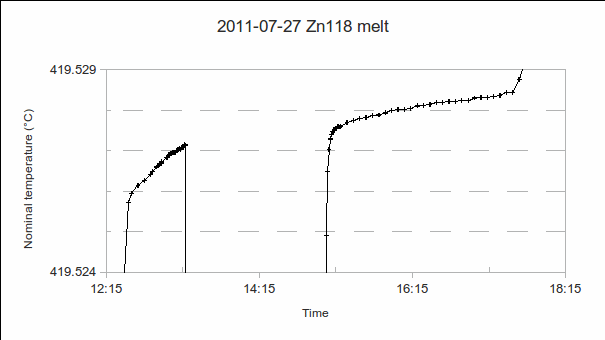
a) Start time: This may be determined after completing the measurement, by studying a graph of PRT1’s readings. (In the example above, it’s 12:35.)

b) PRT1’s resistance at the solidus (start of the melt): This is needed to determine the melting range, that is, the difference from the liquidus (at the end of the melt). (In the example above, it’s 419.526 °C.)

c) End time: As for start time. (In the example above, it’s 17:35, in other words, the melt lasted five hours.)

d) PRT1’s resistance at the liquidus (end of the melt): Additional PRTs may be calibrated during the melt (as in the above example, from 13:20 to 15:00), but the end of the melt should be recorded using PRT1, so that the melting range and melt-freeze coincidence can be accurately determined. (In the example above, it’s 419.528 4 °C. In other words, the melting range is 0.002 4 °C.)

4. “Soak”, when the fixed point material is in the liquid state for several hours, after the melt:

a) PRT1’s resistance, when the temperature has stabilised: Calculate the approximate difference from the melt temperature. (The approximate PRT sensitivity, 0.1 Ω/°C or 0.39 Ω/°C, may be used to convert differences in ohms to °C.) Use this to determine the offset (or error, or correction) of the furnace or bath’s temperature controller. This allows better setpoints to be used next time, more closely approaching the “melt + 5 °C” and “freeze – 1 °C” furnace temperatures commonly desired during melt and freeze. (In the example above, the “soak” temperature is approximately 5 °C above the melt, as desired.)

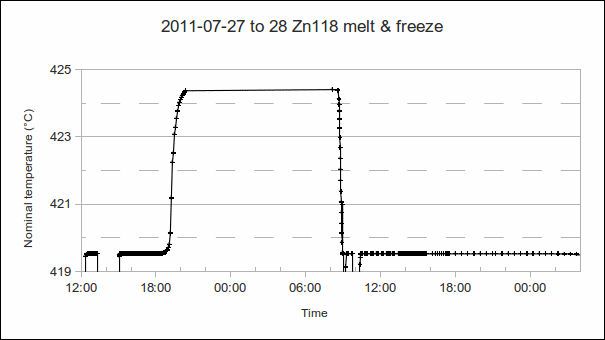
5. Supercool:

a)Time that the setpoint is reduced: This will tell us how long it takes for recalescence to occur. (If it takes too long, the chosen setpoint may be lower next time.)

b) Setpoint used during the supercool: This is usually several °C lower than that during the freeze, to hasten recalescence and the start of the freeze.

c) Time at which recalescence occurs: See a).

d) PRT1’s resistance, at the moment of recalescence: When the liquid starts solidifying, the temperature starts rising out of the supercool. The depth of the supercool (difference from freeze temperature) gives a rough indication of the “condition” (purity?) of the fixed point cell material. (The more impurities, the more easily nucleation occurs and freezing starts, therefore the shallower the supercool.)

(In the example above, the setpoint was reduced at 8:35, the PRT reached a minimum reading of 419.521 °C, and recalescence occurred at 9:00.)

6. Freeze:

a) Start time.

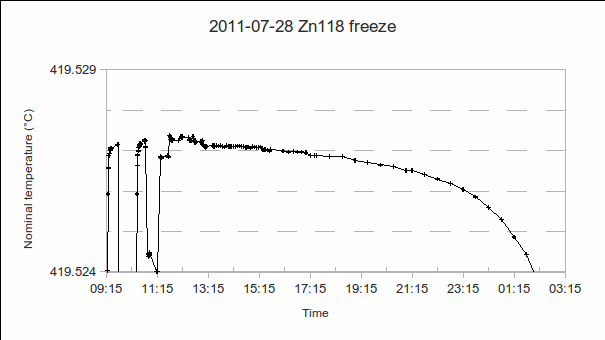
b) PRT1’s resistance at the liquidus (start of the freeze): If plateau shapes are as expected (PRT reading rising as the melt progresses, and falling as the freeze progresses), the melt-freeze coincidence is calculated as . As the furnace temperature is several °C colder during freeze than melt, this difference in PRT readings indicates the sensitivity (if any) of the PRT to the environment outside the fixed point cell.

(In the above example, PRT1 reads 419.527 1 °C from 9:25 to 9:45, then an additional PRT is calibrated from 9:45 to 10:20, and PRT1 reads 419.527 2 °C from 10:30 to 10:45. Freeze – melt = 419.527 2 °C – 419.528 4 °C = -0.001 2 °C.)

c) Self-heating of the PRT: If the resistance measuring instrument allows it, change the current passing through the PRT (preferably by a factor of √2 or 1/√2, so that the power dissipated in the resistance element is conveniently doubled or halved) and note the change in its resistance. (These readings are not shown in the graph above.)

d) Vertical temperature gradients in the cell, during the plateau: These should preferably be evaluated during the plateau where the furnace or bath provides least compensation for stem conduction errors, that is, the freeze, for fixed points above room temperature, or the melt, for fixed points below room temperature.

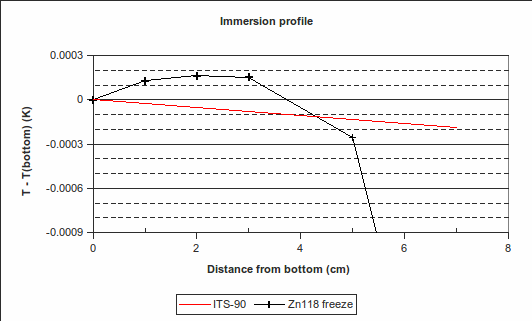
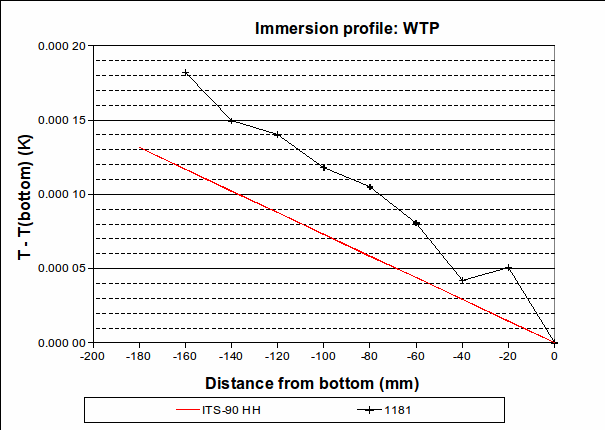
(In the above example, PRT1’s immersion was changed to 70 mm, 50 mm, 30 mm, 20 mm and 10 mm above the bottom of the re-entrant well, from 10:50 to 13:00. Its readings were 419.524 °C, 419.526 8 °C, 419.527 3 °C, 419.527 3 °C and 419.527 2 °C, respectively. Its reading back at maximum immersion was 419.527 1 °C, very close to the value at the start of the freeze, indicating that the zinc cell was still on the freeze plateau. The red “ITS-90″ line in the immersion profile above is the expected variation in freezing temperature caused by a change in depth, according to the hydrostatic head coefficient for zinc published in the ITS-90 Table 2.)

Regarding the sequence of immersion depths: PRT1 is first raised to the highest position, then lowered, step-by-step, back down again. This is because raising the PRT causes some cold air to enter the re-entrant well, temporarily cooling the PRT. To avoid a resulting error, all but one of the measurements are done while increasing the immersion depth.

e) End time.

f) PRT1’s resistance at the solidus (end of the freeze): Additional PRTs may be calibrated during the freeze, but PRT1 should be re-inserted before the end of the freeze, so that the freezing range can be determined. In order to know what time period is available to calibrate other PRTs, record the first melt and freeze (using this combination of fixed point cell and furnace) using just one PRT. Note: If additional PRTs are to be inserted in the fixed point cell, they should be pre-heated (or cooled) to approximately the fixed point temperature, before insertion, to avoid excessive shortening of the freeze plateau.

(As can be seen in the above example, rounding of the plateau makes it difficult to precisely locate the end of the freeze. However, it is the temperature stability during the measurements from 9:25 to 13:00, when additional PRTs, self-heating and immersion measurements were performed, that is most important. The shape of the rest of the plateau is useful as an indicator of furnace temperature uniformity, and, consequently, shape of the solid-liquid interface, as the phase transition progresses, but will not be used in the uncertainty analysis. So, somewhat arbitrarily, the end of the freeze is estimated as 23:15, 419.526 °C, giving a freezing range of about 0.001 °C and a 14-hour freeze plateau.)

DETERMINING THE RESISTANCE RATIO :

The liquidus temperature, when almost all the material is liquid (at the end of the melt or the start of the freeze), is closest to the ideal phase transition temperature [McLaren, “The freezing points of high purity metals as precision temperature standards”, In Temperature: Its Measurement and Control in Science and Industry, Vol. 3, 1962, 185-198]. For all but one of the metal fixed points used to calibrate PRTs (mercury, indium, …, silver), the freeze is usually preferred over the melt. (Gallium is used on the melt, as it has such a large supercool that its freeze cannot be used.) So, for  we will use the value at the start of the freeze (the resistance equivalent to 419.527 2 °C), namely, 65.619 14 Ω.

The phase transition temperature published in the ITS-90 is that at the surface of the fixed point material. The temperature changes with increasing depth, due to the increasing pressure exerted by the column of material above the measurement location. For zinc, this hydrostatic head effect is 2.7 mK/m (“depth” coefficient in ITS-90 Table 2). The mid-point of the PRT sensing element is 155 mm below the surface of the zinc, where it is 0.002 7 °C/m x 0.155 m = 0.000 4 °C hotter than at the surface. The resistance corrected for hydrostatic head is therefore 65.619 14 Ω – 0.000 4 °C x 0.1 Ω/°C = 65.619 10 Ω.

For and , the measured values are 25.547 308 Ω and 25.547 304 Ω, respectively. The hydrostatic head effect in the WTP cell is -0.73 mK/m x 0.265 m = -0.000 19 °C. (Note the difference in sign from zinc: water, unusually, freezes at a lower temperature when the pressure increases.) The resistances corrected for hydrostatic head are 25.547 327 Ω and 25.547 323 Ω, respectively.

The zinc cell was sealed by the manufacturer, with the gas pressure adjusted to be 101.3 kPa at the freezing temperature, so no correction is required for gas pressure.  (The phase transition temperature varies with varying gas pressure above the fixed point material, according to the “pressure” coefficient published in ITS-90 Table 2.) The water cell, being a triple point, should not contain any gas but water vapour, so no gas pressure correction is applied here, either.

So, .

The resistances were measured at 1 mA current. (It is common practice to correct fixed point calibration data to 0 mA current, using the self-heating measurements mentioned above. However, here we do not correct for self-heating, as we plan to use the PRT at 1 mA current without applying self-heating corrections. For interest’s sake, the self-heating of this PRT due to the 1 mA current was 0.000 08 Ω at the zinc point and 0.000 02 Ω at the water triple point: these values are very small, owing to the design of this model of PRT.)

COMPONENTS OF MEASUREMENT UNCERTAINTY [CCT-WG3, “Uncertainties in the realisation of the SPRT subranges of the ITS-90″, CCT/08-19/rev]:

1. Gas pressure: The uncertainty in gas pressure inside a sealed fixed point cell may be estimated as 3 kPa (coverage factor k=1), if no method of measuring it exists [CCT-WG3 guide, section 2.1]. To convert to temperature units, use the gas pressure coefficient of for zinc [ITS-90 Table 2], yielding 0.000 1 °C (k=1). For the WTP cell, the residual gas pressure may be estimated by the inverting the cell and observing how much the remaining gas bubble is compressed [CCT-WG3 guide, section 3.1]: observing a reduction in bubble volume of 100 times, we estimate the effect of the residual gas pressure as 0.000 002 °C (k=1).

2. Hydrostatic pressure: We estimate the uncertainty in immersion depth of the mid-point of the PRT element below the surface of the zinc or water to be 10 mm (k=1). (This uncertainty arises from lack of knowledge of the exact depth of the zinc, as well as thermal expansion inside the fixed point cell and the PRT as the temperature rises.) For zinc, 2.7 mK/m x 0.01 m = 0.000 03 °C (k=1). For the WTP, -0.73 mK/m x 0.01 m = 0.000 007 °C (k=1).

3. Chemical impurities and isotopic composition: Earlier, we mentioned that the liquidus temperature is closest to the ideal phase transition temperature, and chose to use the value at the start of the freeze. The liquidus temperature differs from the ideal temperature because the fixed point material is not completely pure. The zinc cell manufacturer reported the total mole fraction of impurities to be . Using this information, the uncertainty in the liquidus temperature may be estimated using the “overall maximum estimate” (OME) method: , where the cryoscopic constant for zinc, so that (k=1) [CCT-WG3 guide, equation (2.23) and Appendix B]. (The melting range following a slow freeze was previously recommended as an indicator of purity: the purer the material, the narrower the melting range. However, some significant impurities may not betray their presence by an increased melting range, so this range is only used for quality assurance purposes now, to indicate changes in the cell or furnace condition.) For the WTP cell, we have no impurity information, so we use a literature value of 0.000 05 °C (k=1.732) [CCT-WG3 guide, section 3.2]. Likewise, for the isotopic composition of the water, we use a literature value of 0.000 1 °C (k=1.732) [CCT-WG3 guide, section 3.3].

4. Immersion and thermal effects: The vertical temperature gradient measured during the zinc freeze deviates from the expected behaviour by a maximum of 0.000 25 °C over the bottom 30 mm, with the PRT being hotter than expected. (See the difference between the “Zn118 freeze” line and the red “ITS-90″ line in the “Immersion profile” graph above. We choose 30 mm as it is approximately half the length of the PRT element.) However, , suggesting that the lower furnace temperature during the freeze causes the PRT to be colder than expected during that plateau. To be conservative, we will use the larger of these values, 0.001 2 °C (k=1.732), as the uncertainty due to immersion and thermal effects for zinc. For the WTP, the following immersion profile was measured:

The largest deviation from the expected profile, over the bottom 30 mm, is 0.000 036 °C. We use this value as the half-width of a rectangular distribution (k=1.732).

5. Difference from the liquidus point: PRT1 was measured at the end of the melt and at the start of the freeze, that is, at the liquidus point. However, the additional PRTs measured during the melt were 0.001 3 °C to 0.000 8 °C below the liquidus point. (See the melt graph of PRT1, above.) So, the additional PRTs measured during the melt must include an additional uncertainty component of approximately 0.001 °C (k=1.732?) to account for this difference. The one measured during the freeze was at the liquidus point (considering the agreement of PRT1’s readings before and after).

6. PRT oxidation state, crystal defects and strain (variation in ): changes somewhat during the fixed point measurement, because of various causes. The uncertainty component associated with this variation is , which is 0.000 02 °C (k=1.732) in temperature units. The effect of variation in is larger, the higher the temperature: the uncertainty scales according to W(t).

7. Self-heating: We do not correct measured resistances at 1 mA to zero current, therefore we do not include an uncertainty for self-heating.

8. Resistance measuring instrument – non-linearity: The bridge non-linearity has been evaluated as (k=2) in units of bridge ratio. To find the uncertainty in , multiply by , which is 100 Ω, yielding 0.000 02 Ω. Dividing by 0.1 Ω/°C, we obtain 0.000 2 °C (k=2).

9. Standard resistor: The temperature coefficient of is . The maximum variation in its temperature during the measurements is estimated to be 0.2 °C (k=1.732), yielding an uncertainty in of , or 0.000 07 °C (k=1.732).

We want to calculate the uncertainty in resistance ratio . To do this, we first calculate , propagate that to the zinc temperature by multiplying by W(Zn), then combine it with the other components relevant to the zinc point. In doing this, beware of double-counting components: Variation in must be included in the WTP budget (as is), or in the Zn budget (scaled by W(Zn) = 2.569), but not in both. Bridge non-linearity affects the ratio between Zn and WTP readings more than it does the very narrowly varying value, so we only count it once, in the Zn budget. Variation in the temperature of the standard resistor was estimated over the day or so between measurements of and , so is also only counted once.

WTP uncertainty budget:

Component	Value (mK)	Divisor	Sensitivity coeff	u(k=1) (mK)
Gas pressure	0.002	1	1	0.002
Hydrostatic head	0.007	1	1	0.007
Impurities	0.05	1.732	1	0.029
Isotopic composition	0.1	1.732	1	0.058
Immersion	0.036	1.732	1	0.021
Difference from liquidus
Variation in Rtp
Self-heating
Bridge non-linearity
Std resistor
Propagation of u(Rtp)
uc(k=1)				0.062

 

Zn uncertainty budget:

Component	Value (mK)	Divisor	Sensitivity coeff	u(k=1) (mK)
Gas pressure	0.1	1	1	0.1
Hydrostatic head	0.03	1	1	0.03
Impurities	0.3	1	1	0.3
Isotopic composition
Immersion	1.2	1.732	1	0.7
Difference from liquidus	0	1.732	1	0
Variation in Rtp	0.02	1.732	2.569	0.01
Self-heating
Bridge non-linearity	0.2	2	1	0.1
Std resistor	0.07	1.732	1	0.04
Propagation of u(Rtp)	0.062	1	2.569	0.16
uc(k=1)				0.8

The dominant component in the Zn budget is immersion (stem conduction error). As we were very conservative in estimating this component (the value from the immersion profile measurement was five times smaller than the freeze-melt value used), we can safely assume large degrees of freedom in this component, therefore large effective degrees of freedom in the combined uncertainty. So, we multiply by a coverage factor of k=2 to obtain the expanded uncertainty . (Actually, as the dominant component follows a rectangular distribution, we’re entitled to use k=1.65 [EA-4/02 M: 1999, Expression of the Uncertainty of Measurement in Calibration, section S9.14], yielding 0.001 3 K, but let’s be conservative and stick with 1.6 mK.)

(Contact the author at lmc-solutions.co.za.)

This article discusses the calibration of a relative humidity (RH) hygrometer by comparison with a condensation (“chilled mirror”) dewpoint hygrometer and a thermometer measuring air temperature (“dry-bulb temperature”, in humidity parlance). It focuses on estimation of the uncertainty to be associated with the measurement result.
The comparison between the RH hygrometer (Unit Under Test, or UUT) and the dewpoint hygrometer and thermometer (together forming the reference standard) is performed in  a temperature- and humidity-variable chamber. The dewpoint hygrometer measures dew-point (or frost-point, if below 0 °C) temperature, , with an uncertainty of 0.1 °C (coverage factor k=2). A resistance thermometer is used to measure the air temperature, , also with an uncertainty of 0.1 °C (k=2). (No correction is applied for self-heating of the resistance thermometer, as it was calibrated in air, that is, in similar conditions to those in which it is used.) The temperature uniformity of the chamber is specified by the manufacturer to be ± 0.3 °C. (We assume a coverage factor of k = √3.)
Measurements are performed at temperatures of 5 °C, 20 °C and 50 °C, and at relative humidities of 10 %rh, 50 %rh and 90 %rh.

First, we must be able to calculate relative humidity from measured values of dew point and air temperature. Relative humidity is defined as a ratio of water vapour pressures: , where is the actual vapour pressure of water and is the saturation vapour pressure of water at the prevailing temperature [Beginner’s guide to humidity measurement, NPL Good Practice Guide No 124, p 17]. (Here we express RH from 0 to 1, not 0 %rh to 100 %rh.) We will use the Magnus formula to calculate water vapour pressures: , where is saturation water vapour pressure (in Pa) at temperature  (in °C), is used for the irrational number 2.718… (to distinguish it from the symbol for vapour pressure), and the constants are and [Guide to the measurement of humidity, Institute of Measurement and Control, 1996, p 53]. The Magnus formula has an uncertainty of less than 1.0 % (k=2) from -65 °C to 60 °C. We will not apply the water vapour enhancement factor to or , to account for the presence of gases other than water vapour, as it would cancel in the ratio .

How do we determine the actual water vapour pressure, ? It is the saturation water vapour pressure at the dew-point temperature , by the definition of dew point [Beginner’s guide to humidity measurement, p 2]. So, applying the Magnus formula, .

We may also need to calculate dew point from relative humidity and air temperature. To achieve this, first calculate vapour pressure , then manipulate the Magnus formula to obtain [Guide to the measurement of humidity, Institute of Measurement and Control, 1996, p 54].

We will also need the sensitivity coefficients and :

Evaluating the sensitivities at typical temperatures  = -20 °Cfp to 50 °Cdp and  = 5 °C to 50 °C, we see the familiar rule-of-thumb that  or , in other words, RH changes by approximately 6% of the value, for a change of 1 °C in dew point or air temperature. (The symbols °Cfp and °Cdp, for “degrees Celsius frostpoint” and “degrees Celsius dewpoint”, are commonly used to distinguish dew-point temperature, a measure of humidity, from air temperature.) In other words, if  increases from 8 °Cdp to 9 °Cdp (at  = 20 °C), RH changes from 0.46 (or 46 %rh) to 0.49 (or 49 %rh), an increase of 3 %rh, or 6% of value. If  increases from 49 °C to 50 °C (at  = 48 °Cdp), RH changes from 0.95 (95 %rh) to 0.90 (90 %rh), a decrease of 5 %rh, or 6% of value.

Here are the dew points, for the air temperature and relative humidity measurement points mentioned above:

	Air temp: 5 °C	20 °C	50 °C
RH: 10 %rh	-21.8 °Cfp	-11.2 °Cfp	10.1 °Cdp
50 %rh	-4.0 °Cfp	9.3 °Cdp	36.7 °Cdp
90 %rh	3.5 °Cdp	18.3 °Cdp	47.9 °Cdp

We will evaluate uncertainties for the three combinations indicated in bold in the table above.

We estimate hysteresis of the UUT, a capacitive RH sensor, to vary from zero at 10 %rh to 0.6 %rh (k=1) at 50 %rh to zero at 90 %rh.

5 °C, RH = 0.10 (10 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	-21.8 °Cfp	0.05 °C	0.010	0.0005
Air temperature	5.0 °C	0.05 °C	-0.007	-0.0004
Chamber: Temperature gradient		0.17 °C	-0.007	-0.0012
UUT: Hysteresis		0.000 RH	1	0.0000
Combined uncertainty (k=1)				0.0013
U(k=2)				0.003 (0.3 %rh)

 

20 °C, RH = 0.50 (50 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	9.3 °Cdp	0.05 °C	0.034	0.0017
Air temperature	20.0 °C	0.05 °C	-0.031	-0.0015
Chamber: Temperature gradient		0.17 °C	-0.031	-0.0054
UUT: Hysteresis		0.006 RH	1	0.0060
Combined uncertainty (k=1)				0.0083
U(k=2)				0.017 (1.7 %rh)

 

50 °C, RH = 0.90 (90 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	47.9 °Cdp	0.05 °C	0.046	0.0023
Air temperature	50.0 °C	0.05 °C	-0.045	-0.0022
Chamber: Temperature gradient		0.17 °C	-0.045	-0.0078
UUT: Hysteresis		0.000 RH	1	0.0000
Combined uncertainty (k=1)				0.0084
U(k=2)				0.017 (1.7 %rh)

(Contact the author at lmc-solutions.co.za.)

This article will discuss the calibration of a 1 kg weight of class by comparison with a 1 kg weight of class (weight classes are described in OIML R 111-1), using a balance of resolution 0.1 mg. In particular, it will focus on the estimation of uncertainty of measurement (UoM) for this calibration, for which the result is intended to be reported as a conventional mass (as discussed in OIML D 28).

The 80-page document R 111-1 describes many characteristics of weights (for example, construction) that are of limited relevance to the calibration laboratory: we will use mostly the sections on Maximum Permissible Errors (section 5, p 11-12), Density (sections 10, p 17-18 and B.7.9.3, p 58) and, especially, Calibration (Annex C, p 61-70). The 12-page document D 28, “Conventional value of the result of weighing in air”, presents a convenient summary of the information most relevant to calibration.

The conventional mass of a body is equal to the mass of a standard weight that balances this body under “conventional” conditions, namely, ambient temperature = 20 °C, air density and standard weight density [D 28 section 4, p 5]. The conditions have been chosen such that mass, , and conventional mass, , of a weight do not differ “much” [D 28 section 0, p 4]. However, we will see, when we try to achieve the required calibration uncertainty for a 1 kg weight, which is [R 111-1 section 5.2 and Table 1, p 11-12], or, equivalently, a relative standard uncertainty of , that typical deviations of weight density from the conventional can cause significant differences between and .

Note: The subscript “c” indicates “conventional”, “r” refers to the reference weight (in other words, the measurement standard) and “t” refers to the test weight (or Unit Under Test).

The relation between conventional mass and mass is given by [D 28 equation 1, p 6].

In our example, both the reference weight and the test weight are made of stainless steel. The mass of the reference weight is chosen to be , with the largest calibration uncertainty allowed by R 111-1 for class weights. Relevant data are presented in the table below.

Quantity	Uncertainty	Reference
		[R 111-1 Table B.7, p 58]
		[R 111-1 Table 1, p 12]
		[R 111-1 Table B.7, p 58]
Air pressure
Humidity
Air temperature
	(see below for calculation)	[R 111-1 equation (E.3-1), p 76]

Notes:

1.The conventional mass is lower than : this difference is large (compared to the relative uncertainty goal), although the assumed weight density is not far from ideal.

2. As the densities of the reference and test weights are not known, they are “assumed” according to R 111-1 Table B.7 (for stainless steel). Although they are assumed to be the same in most of the data analysis below, the possible difference between the densities must be taken into account in the uncertainty analysis. In particular, during calculation of the uncertainty in the air buoyancy correction , the sensitivity coefficient of will be calculated using the worst-case scenario: as for 1 kg weights and for 1 kg weights [R 111-1 Table 5, p 17], the sensitivity coefficient will be used. (The calculation is performed below.)

3. The air pressure , and, consequently, air density , are unusually low, because the measurements were performed at an altitude of 2400 m. The even-more-approximate formula for air density, [R 111-1 equation (E.3-2), p 76], yields a similar air density, .

The uncertainty in air density is calculated as follows: . Sensitivity coefficients come from R 111-1 section C.6.3.6 (p 68), with and being converted from  to  and from fractional relative humidity to %rh, respectively. (Both change by a factor of 100, though in opposite directions.) It is clear that air pressure has the largest effect on air density, followed by temperature, with the effect of relative humidity being negligible.

The conventional masses of test and reference weights are related as follows:

[D 28 equation (9), p 8],

where is the measured difference in apparent masses.

The air buoyancy correction  [D 28 equation (10), p 8] is applied, because the air density differs from by more than 10 % [R 111-1 section 10.2.1, p 18].

To determine the uncertainty , we’ll need the sensitivity coefficients , and .

Then, , where (the uncertainty of the weighing process and the balance, combined) and , in the notation of R 111-1 section C.6, p 66-70.

Expressed as a relative uncertainty, .

From the table above, .

From equation (C.6.3-1) of R 111-1 (p 67), ,

where is the air density during the last calibration of the reference weight.

Using , + . So, , with the terms in and dominating over the term in .

The term contains the uncertainty of the weighing process, , which is an ESDM calculated as 0.01 mg, the sensitivity of the balance, , and the display resolution of the balance, . (Eccentric loading of the balance is included in , and magnetism is negligible, according to p 69 of R 111-1.) In total, let’s suppose that , so that .

Finally, . So, we have achieved our goal of a relative standard uncertainty smaller than .

(Contact the author at lmc-solutions.co.za.)