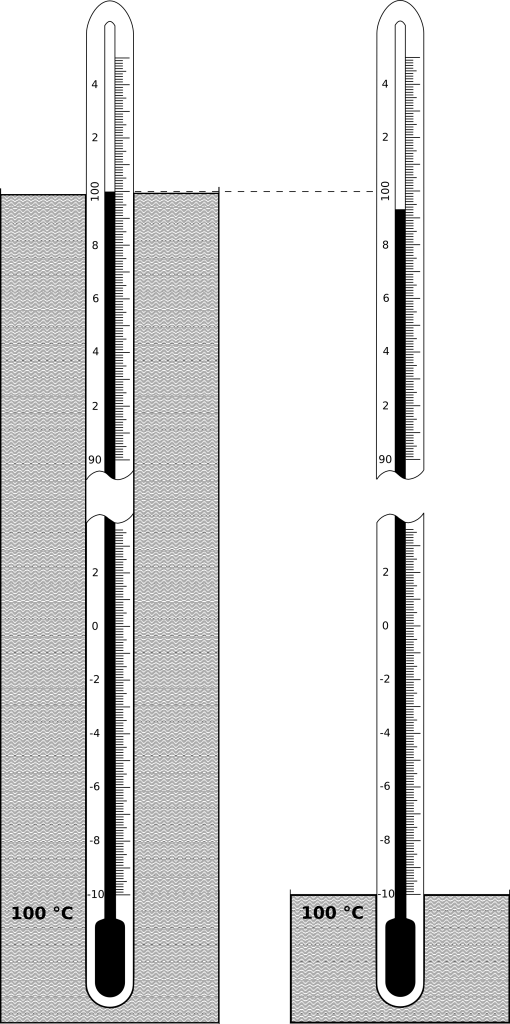
A liquid-in-glass (LIG) thermometer uses the thermal expansion of a liquid as the thermometric property. If the immersion depth of the thermometer in the medium of interest is changed from total to partial, the temperature of a part of the liquid column changes, its volume changes (because of thermal contraction or expansion), and the reading of the thermometer changes. (Note: This only happens if the medium of interest is at a different temperature from the surroundings. The further from room temperature is the medium of interest, the larger is the effect.)

Consider the mercury-in-glass thermometer in the sketch above: At total immersion, all of the mercury is at the bath temperature (100 °C) and the reading is 100.0 °C. When its immersion is reduced to the -10 °C mark, much of the liquid column is outside the bath (this is the “emergent” liquid column), at an average temperature somewhere between the bath temperature (100 °C) and room temperature (20 °C). (It is typically closer to room temperature than to the bath temperature.) Being at a lower temperature, its volume is less, and therefore the thermometer reading is lower (99.3 °C).

Q: Can we calculate how much the thermometer reading will change, with a change in immersion?

A: Yes, if we know the thermal expansion coefficient of the liquid (K), the length of the Emergent Liquid Column (N, expressed in °C on the thermometer scale), and the difference between the temperatures of the liquid column in the two cases (T[LC1] – T[LC2]). Then, the difference in thermometer readings between case 1 (total immersion) and case 2 (partial immersion) is K x N x (T[LC1] – T[LC2]).

The thermal expansion coefficient of mercury is K = 0.00016 per °C. (It’s about six times larger, 0.001 per °C, for ethanol.)

The length of the ELC in the partial immersion case is N = 100 °C – (-10 °C) = 110 °C. (To be precise, it is 109.3 °C, but an error of one percent is quite acceptable in such a calculation.)

In case 1 (total immersion), the liquid column is at the same temperature as the bath, that is, T[LC1] = 100 °C. In case 2 (partial immersion), we make a crude approximation, that the ELC is halfway between the bath temperature and room temperature, T[LC2] = (100 °C + 20 °C) / 2 = 60 °C. So, T[LC1] – T[LC2] = 40 °C. (As noted above, the actual average ELC temperature will be closer to room temperature than this crude estimate.)

Therefore, reading(1) – reading(2) = 0.00016 per °C x 110 °C x 40 °C = 0.7 °C.

Q: In which case is the thermometer reading higher? (Or, in which direction should we apply the ELC correction?)

A: In that situation where the liquid column is hotter, the thermometer reading will be higher. (In the above example, the reading will be higher in case 1, at total immersion.)

Q: In the above example, we determined the difference between readings at total and partial immersion. Can we determine the difference between two different partial immersions?

A: Yes. Such a calculation may be performed by correcting from partial immersion 2 to total immersion (let’s continue calling total immersion “situation 1″), then from total immersion to partial immersion 3. However, if we make the approximation that the differences in ELC temperatures (T[LC1] – T[LC2] and T[LC1] – T[LC3]) are equal, then we can calculate the difference between situations 3 and 2 directly, as K x (N[2] – N[3]) x (T[LC1] – T[LC2]).

For example, if the immersion depth in situation 3 was up to the 70 °C mark, then the difference in reading from situation 2 (immersion to the -10 °C mark) would be approximately 0.00016 per °C x (110 °C – 30 °C) x 40 °C = 0.5 °C. In such conversions between different partial immersions, it is particularly important to check the direction of the correction using common sense: as the liquid column is hotter in situation 3 than in 2, the reading will be higher by 0.5 °C.

Q: How accurate are such ELC corrections?

A: The thermal expansion coefficient (K) and length of the ELC (N) are usually known quite accurately (uncertainties of 2-4% at coverage factor k=2), but (T[LC1] – T[LC2]) might only be known with an uncertainty of 10% (k=2) if measured [Nicholas & White, Traceable Temperatures, p 275] or 50% (k=2) if crudely estimated as described above.

The best solution is to have the thermometer calibrated at the same immersion depth at which it is used. Even if the ELC temperature is not very accurately known, it is quite likely to be the same during calibration and during use, so that the calibration results can be applied by the user with a small uncertainty.

If calibration is performed at partial immersion, the calibration laboratory should estimate the average ELC temperature. The tips of two thermometers (LIG, thermocouple or PRT) may be placed at the surface of the liquid bath and at the top of the liquid column, respectively, and the average of the two measured temperatures used as the average ELC temperature. Although heat transfer may be quite different in the LIG thermometer and around the two other thermometers, this method may estimate (T[LC1] – T[LC2]) to an uncertainty of perhaps 20% (k=2).

It may be advisable for the calibration laboratory to report the uncertainty in average ELC temperature separately from other uncertainty components. In this way, the user can still benefit from a small uncertainty, if he uses the thermometer at the same immersion depth as that during calibration.

If the user must use the thermometer at an immersion depth significantly different from that during calibration, he must be prepared to accept an uncertainty of 10-50% (coverage factor k=2) in ELC correction, depending on how accurately the average ELC temperature is estimated. Using our crude estimation of T(LC2), the correction from case 1 to case 2 would be -0.7 °C ± 0.35 °C, at a coverage factor of k=2. If we had measured T(LC2), the uncertainty in the ELC correction might have been 0.14 °C (or 20%, in relative terms).

Exercises:

1. Calculate the reading at partial immersion (to the -10 °C mark) in the sketch above, if the thermometer liquid was ethanol (thermal expansion coefficient K = 0.001 per °C) instead of mercury.

2. Calculate the uncertainty in the ELC correction you have just determined for this alcohol-in-glass thermometer, if T[LC1] – T[LC2] = 40 °C ± 20 °C (coverage factor k=2).

3. An alcohol-in-glass thermometer reads -30.8 °C at total immersion. What is the reading if its immersion is reduced to the -50 °C mark and the average ELC temperature at partial immersion is measured as 10 °C?

(Contact the author at lmc-solutions.co.za.)