Category Archives: Articles

Articles of MetrologyRules

Conformity to specification – calculating risk and implementing a decision rule in Excel or Calc

March 6, 2022 Hans Liedberg 2 Comments

When reporting a measurement result, a calibration or testing laboratory may state whether or not it conforms to a certain specification. When reporting whether the result is a “pass” or a “fail”, the laboratory must clearly describe how it accounts for measurement uncertainty in making its decision. (This description of how uncertainty is treated is called a “decision rule”.)
Section 7.8.6 of ISO/IEC 17025:2017 requires the laboratory to “tak(e) into account the level of risk (such as false accept…)”. Guidance on decision rules and the associated risk to the customer may be found in ILAC-G8:09/2019 “Guidelines on Decision Rules and Statements of Conformity” and JCGM 106:2012 “Evaluation of measurement data – The role of measurement uncertainty in conformity assessment”. We will assume that the customer mostly wishes to avoid a “False Accept”, and will therefore calculate the “Probability of False Accept” (PFA) [ILAC-G8 5.2], for which some maximum acceptable value should be agreed between laboratory and customer. We will also determine which statement (“pass”, “fail”, “conditional pass” or “conditional fail”, as per ILAC-G8 4.2.3) to report for a particular guard band. These calculations will be performed using commonly available spreadsheet functions.

We will assume that measured results follow a normal (or Gaussian) distribution, with standard deviation equal to the estimated standard uncertainty, u(k=1). (Note that if the dominant uncertainty component is not normally distributed, the combined uncertainty is unlikely to be [EA-4/02 S8.3], so this assumption will be inappropriate.)
We will use the same numbers as the example in JCGM 106 7.4, so we can check our answers against theirs: result = 13.6, u(k=1) = 1.8, tolerance limits TL = 12.5 and TU = 16.3.

Spreadsheet programs such as Microsoft Excel and LibreOffice Calc include functions that operate on the “standard” normal distribution, which has a mean of 0 and a standard deviation of 1: (The probability density function below is plotted using the spreadsheet function NORM.DIST, with arguments x = -3 to 3, mean = 0, stdev = 1, Cumulate? = 0.)

However, the normal distribution we start with has a mean equal to the measured result, and a standard deviation equal to the combined standard uncertainty, u(k=1):

How do we scale and move our distribution, so it becomes a “standard” one, so that we may use the available spreadsheet functions? (In particular, what do the tolerance limits become, when we transform the distribution?): We subtract the result from the x-values (to centre the distribution around 0), and divide by u(k=1) (to change its “width” to 1): TL’ = (TL – result) / u = -0.61 and TU’ = (TU – result) / u = 1.50.

Now, how do we find the probability that the true value lies within the tolerance limits?: We find the area under the curve of the “standard” normal distribution, between the new tolerance limits, using the function GAUSS, which integrates from 0 to the given value. (The total area under the curve, from -∞ to ∞, is 1.00.): “Probability of True Accept” (PTA) = GAUSS(TU’) – GAUSS(TL’) = GAUSS(1.50) – GAUSS(-0.61) = 0.663 = 66.3%. (As the GAUSS function integrates from 0 to a value, it must be applied twice, to obtain the areas to the right and to the left of the mean value. The subtraction is because the value of the 2nd term is negative, while we need it to be positive.) This probability agrees with that found in JCGM 106 7.4, indicating that we probably performed the calculation correctly.
The “Probability of False Accept” (PFA) is 1.00 – PTA = 1.00 – 0.663 = 0.337 = 33.7%.

Now, we will implement a “Non-binary Statement with Guard Band”, as per ILAC-G8 4.2.3, using the spreadsheet functions IF, AND and OR to determine whether the statement of conformity should be “Pass” (result within acceptance interval, with guard bands w = rU, where U is the expanded uncertainty and r = 1 leads to PFA < 2.5%), “Fail” (result outside tolerance, with Probability of False Reject < 2.5%) or “Conditional” Pass or Fail (as per Fig 5 in ILAC-G8, reproduced below).

By nesting several IF(test, value_if_TRUE, value_if_FALSE) functions, all four conditions are identified:
IF(OR(result + r*U < TL, result - r*U > TU), “Fail”, IF(AND(result – r*U >= TL, result + r*U <= TU), "Pass", IF(AND(result >= TL, result <= TU), “Conditional pass”, “Conditional fail”))). Contact the author at LMC-Solutions.co.za.

Comparing temperature sensors in an unstable environment: the effect of response time

August 14, 2018 Hans Liedberg Leave a comment

When we calibrate a temperature sensor by comparing it to a reference standard thermometer, we try to keep the comparison medium (hereafter called the “environment”) stable in temperature during the period of comparison. (By “stable”, we mean that the fluctuation in the temperature of the environment is small relative to the desired uncertainty of calibration.) But, what happens if the environment temperature does vary significantly during the process of recording reference standard and unit under test (UUT) readings? This article discusses the comparison of temperature sensors with different response times in an unstable environment. It reports measurements of time constants of several types of sensors, and their comparison in a stirred water bath with large temperature fluctuations (on-off, rather than PID, control). The appropriate choice for the uncertainty contribution arising from temperature instability is then justified by an analysis of the measured data.

Temperature sensors do not respond instantaneously to changes in the temperature of the environment they are intended to measure. If a sensor is plunged into an environment, the rate at which the sensor temperature approaches that of the environment is described by Newton’s law of cooling, which leads to the equation
$\displaystyle T - T_{env} = (T_{init} - T_{env}) \cdot e^{-t/t_0}$ (1)
[J. V. Nicholas, D. R. White, Traceable Temperatures, 2nd ed, 2001, p 141], where $\displaystyle t$ is the time since the sensor was plunged into an environment of temperature $\displaystyle T_{env}$ , $\displaystyle T_{init}$ is the initial temperature of the sensor, and $\displaystyle t_0$ is the time constant.
$\displaystyle t_0$ is the time the sensor takes to undergo ~63% of the total change in temperature. It is a function of the heat capacity, $\displaystyle m \cdot c_p$ , of the sensor and the heat transfer coefficient, $\displaystyle h$ , from environment to sensor: $\displaystyle t_0 = \frac {m \cdot c_p}{h \cdot A}$ . It may be determined by measuring $\displaystyle (T - T_{env})$ versus $\displaystyle t$ and modelling the data using equation (1).
(Note that, although the heat capacity is constant for a particular sensor, the heat transfer coefficient varies according to the environment, so that the time constant of a sensor in still air may be tens of times longer than the time constant of the same sensor in stirred water.)

Infrared radiation (non-contact) thermometers typically respond very quickly (response time < 1 s), but this article focuses on immersion probes, which are in physical contact with the environment. The sensors studied were a mineral-insulated, metal-sheathed (MIMS) platinum resistance thermometer (PRT) and type K thermocouple, an epoxy-coated NTC thermistor and a ceramic-sheathed type S thermocouple, with a brief mention of a solid-stem mercury-in-glass thermometer.

First, the time constants were determined by plunging the sensors from an ambient temperature of 15 °C into a stirred water bath controlled at 70 °C. The temperature readings of the PRT are plotted vs time, below:

Equation (1) was manipulated to allow a straight line to be fitted:
$\displaystyle ln(T_{env} - T) = ln(T_{env} - T_{init}) + \frac{-1}{t_0} \cdot t$ (1a)
The linearised data and fitted straight lines are plotted, below:

The following time constants were found. (Time is in units of days in the straight lines fitted to the data above, therefore, so is $\displaystyle t_0$ . It is converted to seconds in the table below.)

Sensor	t0 (seconds)
6.4 mm diameter MIMS PRT	4.3
6 mm diameter MIMS type K thermocouple	2.8
Epoxy-coated NTC thermistor	4.5
6.7 mm diameter ceramic-sheathed type S thermocouple	13.0

The following points were noted:
1. The multimeter used to measure both RTD resistances and thermocouple voltages was set to a slow measurement rate (signal integration over 5 power line cycles or 0.1 s), which may have affected the measured values somewhat.
2. The longer time constant of the ceramic-sheathed type S thermocouple is expected, as the alumina ceramic is less thermally conductive than a metal sheath, there is an air gap between this sheath and the twin-bore alumina insulator holding the thermocouple wires, and these wires are probably thicker (0.4 mm) than those in, for example, the MIMS type K thermocouple. Such a high-temperature laboratory standard thermocouple construction is expected to exhibit the longest time constant of the sensors typically calibrated in a temperature calibration lab.
3. The results show fair agreement with previous measurements of $\displaystyle t_0$ = 5.2 s and 2.9 s, for a heavier 6.4 mm MIMS PRT and a 6.25 mm solid-stem mercury-in-glass thermometer, respectively.

The water bath controller was then adjusted from PID to on-off control, resulting in a control cycle of ±0.5 °C with a period of ~140 s. The following measurements were recorded from the four sensors (vertically offset on the graph, for greater clarity):

From these 58 measurements, over 10 control cycles (23 minutes), the following results were obtained. (Fluctuation in the absolute temperature reading of each sensor is labelled “abs” in the table below. The PRT was considered as the reference standard: the mean deviations of the other sensors relative to the PRT, labelled “dev” below, would be the results reported in their calibration certificates. The experimental standard deviation of the mean, or ESDM, is $\displaystyle \frac{stdev}{\sqrt{n}}$ , where $\displaystyle n$ is the number of readings.)

	PRT	Type K		NTC		Type S
	abs	abs	dev	abs	dev	abs	dev
Mean_all (°C):			0.65		-0.50		-1.19
Std dev (°C):	0.29	0.31	0.12	0.30	0.07	0.25	0.11
ESDM (°C):	0.04	0.04	0.02	0.04	0.01	0.03	0.01

A sample of six measurements was taken from these 58, representing a data set that might be captured during a typical calibration:

	PRT	Type K		NTC		Type S
	abs	abs	dev	abs	dev	abs	dev
Mean_sample (°C):			0.68		-0.48		-1.15
Std dev (°C):			0.15		0.10		0.04
ESDM (°C):			0.06		0.04		0.02
Mean_smp – mean_all (°C):			0.03		0.02		0.04

The following points were noted:
1. The standard deviations of the “absolute” readings are smaller for those sensors with longer time constants (particularly, the type S thermocouple). This is as expected: the sensor response to a sinusoidally varying input is attenuated as the time constant becomes larger relative to the period of oscillation. (In other words, a sensor with more thermal inertia will exhibit less peak-to-peak variation in reading, the faster the control cycle.)
2. The mean of the 10% sample agrees with the mean of all 58 measurements (considered representative of the population) within approximately the ESDM of the sampled deviations: this level of agreement between the sample mean and the population mean suggests that the ESDM of the deviations is the appropriate value to use for the uncertainty component “temperature instability”.
3. The standard deviation of the absolute readings (~0.3 °C, as expected for a control cycle of ±0.5 °C) is about three times larger than the standard deviation of the deviations. Using the standard deviation of the absolute readings of the UUT (or, even more so, the standard deviations of the absolute readings of both reference standard and UUT) as the value(s) for “temperature instability” in the uncertainty budget would overestimate this contribution to the total uncertainty of calibration.

The period of oscillation of the environment’s temperature (~140 s) was long relative to the time constants of the sensors (3 to 13 s). In such a situation, a lag error of up to ~[(13 – 3) s * 0.01 °C/s] = 0.1 °C might exist between the slowest and fastest sensors evaluated, during a part of the control cycle when the environment temperature was monotonically falling or rising. (The rate of cooling is ~0.01 °C/s in the above data, and the rate of heating somewhat faster.) However, provided that the recorded data originate from varying points along the control cycle (not always when the reference standard is rising, for example, but equally often when it is rising and when it is falling), the fluctuation in the difference between reference standard and UUT provides an adequate estimation of the uncertainty contributed by the unstable environment. (The slow sensor will be colder than the fast sensor while the environment is heating, and hotter than the fast one while the environment is cooling: using enough measurements, taken randomly during several control cycles, the average of the differences between the slow and fast sensor will cancel out the effect of differing response time.)

Contact the author at LMC-Solutions.co.za.

Uncertainty of measurement: pressure dead-weight tester

February 11, 2017 Hans Liedberg 2 Comments

Pressure dead-weight testers (DWTs), also known as pressure balances or piston gauges, are used as reference standards for high-accuracy calibration of hydraulic and pneumatic pressure gauges (as well as other DWTs, via the technique of cross-floating). This article estimates the uncertainty of calibration of a pressure gauge by comparison with such a DWT, identifying the uncertainty components that are typically dominant.

The principle of the dead-weight tester is that the pressure exerted by the fluid (usually oil or air) is balanced by a known weight applied to a known surface area (pressure = force / area).

The known weight is provided by calibrated masspieces, together with knowledge of local gravity. The effective area of the piston-cylinder assembly is determined by dimensional measurement, or by comparison with other pressure standards (e.g., cross-floating).

The equation for gauge pressure measured by a DWT is $\displaystyle p = \frac{\left( \sum_i m_i \right) \cdot g \cdot (1-\rho_a / \rho_m) + \tau \cdot \pi d}{A_0 \cdot (1 + \lambda p) \cdot \left(1 + (\alpha + \beta) \cdot (t - 20 \textdegree \mathrm{C}) \right)} + (\rho_{fl} - \rho_a) \cdot g \cdot h$ .

$\displaystyle \sum_i m_i$ is the combined mass of the piston, sleeve (weight carrier) and the weights used. The uncertainty of calibration may be $\displaystyle \frac{U(m)}{m} \approx 10 \cdot 10^{-6}$ (around F2 level). Gravitational acceleration, $\displaystyle g$ , may be measured to better than $\displaystyle 10^{-6}$ , in which case its uncertainty is negligible. However, if it is estimated by a formula, $\displaystyle \frac{U(g)}{g}$ may be $\displaystyle 50 \cdot 10^{-6}$ , which is significant. The certificate typically reports conventional masses, so the buoyancy correction $\displaystyle (1-\rho_a / \rho_m)$ uses conventional air and weight densities (1.2 kg.m^-3 and 8000 kg.m^-3), not the actual ones. The buoyancy correction is around $\displaystyle 150 \cdot 10^{-6}$ : the additional correction $\displaystyle (1.2 - \rho_a) / \rho_m$ for deviation from conventional air density, and its uncertainty, is often negligible ( $\displaystyle \leq 5 \cdot 10^{-6}$ below 300 m altitude).

The surface tension correction, $\displaystyle \tau \cdot \pi d$ , is unimportant for pneumatic systems. For hydraulic ones, the contribution to total weight may be $\displaystyle 14 \cdot 10^{-6}$ , important to correct for, but whose uncertainty has a negligible effect.

The effective area at zero pressure, $\displaystyle A_0$ , has an uncertainty around $\displaystyle 70 \cdot 10^{-6}$ : this is usually the dominant component of total DWT uncertainty, especially at high pressures. The pressure distortion coefficient, $\displaystyle \lambda$ , is ~ $\displaystyle 1 \cdot 10^{-6}$ per MPa, i.e., the correction goes up to $\displaystyle 500 \cdot 10^{-6}$ at 500 MPa. Say its uncertainty is 10% of its value, i.e., up to $\displaystyle 50 \cdot 10^{-6}$ . This may be significant at very high pressures, but is negligible compared to $\displaystyle \frac{U(A_0)}{A_0}$ at lower pressures. The thermal expansion coefficient, $\displaystyle (\alpha + \beta)$ , is ~ $\displaystyle 11 \cdot 10^{-6}$ per °C. So, for $\displaystyle U(t)$ ~1 °C, the contribution to $\displaystyle \frac{U(p)}{p}$ is around $\displaystyle 11 \cdot 10^{-6}$ , which may be significant.

For pneumatic systems, where $\displaystyle \rho_{fl}$ is ~1000 times smaller than for oil, the head correction, $\displaystyle (\rho_{fl} - \rho_a) \cdot g \cdot h$ , is often negligible. The uncertainty in the head correction is typically dominated by $\displaystyle U(h)$ , i.e., $\displaystyle U(\rho_{fl})$ and $\displaystyle U(g)$ are negligible. If h~0.27 m (as in the Fluke P3830 pressure balance) and $\displaystyle U(h)$ is 0.025 m (25 mm, which is not very conservative), the effect on $\displaystyle \frac{U(p)}{p}$ at 4 MPa(g) is $\displaystyle 56 \cdot 10^{-6}$ , one of the two largest contributors. At higher pressures, the $\displaystyle \frac{m}{A_0}$ term dominates and U(head) becomes less important (e.g., $\displaystyle 3 \cdot 10^{-6}$ contribution to $\displaystyle \frac{U(p)}{p}$ at 70 MPa(g)).

In conclusion, the following DWT uncertainty contributors may be significant, and should be included in the uncertainty budget (UB):

$\displaystyle U(m)$ (sensitivity coefficient = $\displaystyle p/m$ )
$\displaystyle U(A_0)$ (sensitivity coefficient = $\displaystyle p/A_0$ )
$\displaystyle U(t)$ (sensitivity coefficient = $\displaystyle p \cdot (\alpha + \beta)$ )
for hydraulic systems, $\displaystyle U(h)$ (sensitivity coefficient = $\displaystyle \rho_{fl} \cdot g$ )

The resolution, hysteresis and zero stability of the gauge being calibrated should also be included in the UB, and will often dominate the combined uncertainty (especially at low pressures).

(Contact the author at lmc-solutions.co.za.)

Control of measuring equipment – the requirements of ISO 9001

January 7, 2017 Hans Liedberg 3 Comments

Once a measuring instrument is purchased and successfully installed in an ISO 9001 certified organization, the responsible staff member might consider his job done. However, to satisfy ISO 9001’s requirements for control, measuring equipment used for product and process verification requires attention throughout its lifespan. This article discusses what needs to be done, and how to do it thoroughly, but cost-effectively. (Note: Clause numbers below are from ISO 9001:2008.)

In section 7 (Product realization) of ISO 9001, clause 7.6 deals with “Control of monitoring and measuring equipment”. Firstly, it states the purpose of monitoring and measuring, namely, “to provide evidence of conformity of product to determined requirements”.

“Where necessary to ensure valid results, measuring equipment shall
a) be calibrated or verified, or both, at specified intervals, or prior to use, against measurement standards traceable to … national measurement standards… the organization shall assess and record the validity of the previous measuring results when the equipment is found not to conform to requirements… Records of the results of calibration and verification shall be maintained.”

Basically, the equipment user must manage his risk of making incorrect measurements (“control”). As zero risk is impossible (risk management = “tolerable” risk), he must also be able to assess the impact when measuring equipment is found to have drifted outside required limits. As in all quality management systems (QMS), record-keeping is essential.

“Verification” means “provision of objective evidence that a given item fulfils specified requirements” [International vocabulary of metrology (VIM), clause 2.44]. In this case, the item is a measuring system that is required to be sufficiently accurate. (To be more precise, the measurement results must be traceable to a national measurement standard, with a small enough measurement uncertainty.)

The equipment user must decide the interval between calibrations or verifications, taking into account regulations, conditions of use, advice from measurement experts, etc.

A calibration or verification is “traceable” [VIM, 2.41] when it is
(i) performed by competent personnel,
(ii) according to a documented & validated procedure (work instruction, SOP),
(iii) using traceable measuring equipment,
(iv) with a proper estimation of measurement uncertainty.

(i) How are personnel proven to be competent? By suitable training records.
(ii) How is a calibration procedure validated? By data, showing the capability of the personnel, procedure and equipment to achieve the claimed measurement uncertainty. Typically, a proficiency test (“PT”) or interlaboratory comparison is carried out.
(iii) How is the measuring equipment used to perform calibration (“measurement standards”) made traceable? It is itself calibrated, by
1) a National Metrology Institute (NMI) with a suitable Calibration and Measurement Capability (CMC) for this parameter published in the BIPM Key Comparison Database (KCDB), or,
2) a calibration lab accredited to ISO 17025 by an ILAC affiliate [ILAC P10:01/2013, sections 2 & 3].
(iv) How is the uncertainty of measurement estimated? The calibration procedure usually lists the main components of uncertainty and describes the manner in which they may be estimated. These components are combined using an internationally agreed method [EA-4/02 Evaluation of the Uncertainty of Measurement in Calibration].

Note the distinction between
a) measuring equipment used for product and process verification, and
b) measuring equipment used to perform calibration (“measurement standards”).
Item b) might be, for example, a “master gauge” used to check (calibrate or verify) other gauges in the factory: This measurement standard’s traceability should satisfy ILAC requirements, including accreditation of the calibrating laboratory to ISO 17025.
Item a) is all the other gauges used in the factory: These items may be calibrated “in-house” (even if the organization is not accredited as a calibration laboratory), but the process must still satisfy requirements (i) to (iv) [SANAS TR 25, section 3.3].

How to satisfy ISO 9001’s calibration/verification requirement in a cost-effective manner:

1. If possible, consider this “continuing cost of ownership” aspect when selecting which equipment to purchase. (This applies not only to measuring equipment, but also to the systems in which they are installed.) For example, sensors with “standard” dimensions and fittings will probably fit more easily into calibration apparatus. An additional access port, allowing connection of a measurement standard next to the working measuring equipment, may allow in situ calibration, saving downtime and effort.

2. Choose measuring equipment with appropriate drift specifications: better specs than necessary will mean unjustified extra expense, while equipment with poor specs will require more frequent calibration/verification with attendant wastage of time and money. This highlights the value of understanding how the various uncertainties in system behaviour affect the time or cost of the process and the quality of the final product. For example, it is probably not useful to install a temperature sensor accurate to 0.1 °C if the temperature controller has a cycle of ±5 °C; a sensor accurate to 1 °C or 1.5 °C would probably do.

3. Consider cost and manhours when choosing external (accredited) or in-house calibration. Remember that in-house calibration requires personnel to be trained, a procedure (including estimation of measurement uncertainty) to be documented, measurement standards to be available and records to be kept. Most organizations adopt a “hybrid” approach: Master gauges, and equipment requiring complex calibration procedures, are calibrated by an external, ISO 17025-accredited, calibration laboratory. Low-accuracy, simple (“factory floor”) measuring equipment is calibrated in-house.
This approach is practical, as the organization’s own personnel need not undergo high-level metrology training, and it is cost-effective, as expensive, high-accuracy, measurement standards need not be maintained in-house, while the bulk of measuring equipment need not be submitted to costly external calibration.

An example – Calibration of Resistance Temperature Devices (RTDs):

The organization chooses to purchase one master RTD with digital display (“master thermometer”). They have it calibrated by an ISO 17025-accredited calibration laboratory, over their operating temperature range (-40 °C to 200 °C), with a calibration uncertainty of 0.1 °C. They decide to send it out for recalibration annually, as the manufacturer’s one-year drift specification for the display is 0.2 °C, and they want to use it to calibrate their working RTDs to an uncertainty of ≤ 0.3 °C.

They also procure a one litre, wide-mouth vacuum flask and an ice crusher, so that they are able to prepare an ice point from available ice cubes and tap water. After experimenting on how best to achieve this with their equipment, they prepare a procedure describing preparation of the ice point and measurement of an RTD therein. The procedure highlights sources of error which may significantly affect the result and explains how to prevent or detect such errors. It also explains how to estimate the uncertainty of calibration of the RTD.

Having received their master thermometer with its calibration certificate, they measure it at the ice point according to their procedure (and estimate the uncertainty of measurement). They then prepare a report comparing their result to that of the external, accredited calibration laboratory at 0 °C: this constitutes an interlaboratory comparison (ILC), demonstrating the measurement capability of their personnel, procedure and equipment when calibrating an RTD in an ice point. The senior staff member files this ILC report in his training records, as evidence of his competence. Junior staff members then compare their own measurement results to that of the senior staff member (intra-laboratory comparison), with the criterion for acceptance being that the results agree within the combined uncertainties. Based on this documented evidence, the organization authorises the relevant staff members to perform in-house calibration of RTDs.

The junior staff members then perform in-house calibration of the organization’s working RTDs at 0 °C every three months (the interval being chosen to adequately manage the risk of measurement error) and record the results in a controlled document, with control limits of ±0.3 °C being imposed. (In other words, a working RTD passes if it reads between -0.3 °C and +0.3 °C at the ice point.) The working RTDs are of tolerance class C, that is, at the time of manufacture they complied with the temperature/resistance tables published in IEC 60751 within ±(0.6 + 0.01∙|t|) °C, over the range (-50 to 600) °C. As RTDs falling within these limits are acceptable to the organization, the single-point calibration/verification demonstrating compliance at 0 °C (difference < 0.3 °C, with expanded uncertainty of 0.3 °C) is judged to be sufficient to control temperature measurement accuracy over the full range of operation. (The master thermometer is calibrated over this full range, in case any working RTD exhibits suspicious results and it is desired to perform further evaluation at other temperatures.)

(Contact the author at lmc-solutions.co.za.)

Uncertainty of measurement: water vapour transmission of materials

April 1, 2016 Hans Liedberg Leave a comment

The rate at which water vapour is transmitted through a sheet material is important, for example, if the sheet is to be used to damp-proof a building. The documentary standards ASTM E96 and SANS 952-1 describe methods of evaluating water vapour transmission (WVT), using a desiccant or water to establish a humidity gradient across the sheet. The following article will briefly describe the method, and then focus on estimation of the uncertainty of the calculated WVT value.

The Desiccant Method [E96 clause 4.1] involves sealing the specimen to be tested over the mouth of an impermeable test dish, with desiccant (anhydrous calcium chloride) inside. This dish is placed inside a test chamber or enclosure, where the temperature and humidity are controlled at (38 ± 1) °C and (95 ± 5) %rh [952-1 clause 6.11.1.5], for example. The dish is briefly removed from the chamber and weighed, periodically, over a period of several days. The mass gain indicates the amount of water vapour moving through the specimen into the desiccant. Typically, three specimens are tested [E96 clause 9.1], with a fourth “dummy” (control) specimen mounted on a dish and weighed, but without any desiccant or water in the dish to maintain a humidity gradient [E96 clause 9.6]. The mass change of the dummy is subtracted from the change in each of the test specimens, to cancel out the effect of variations in temperature and air buoyancy [E96 clause 11.3]. (In practice, vigorous air circulation within the test chamber, required to keep the surrounding air uniform in temperature and humidity [E96 clause 6.2], causes the dummy to gain significant mass, too, because it was sealed at a lower ambient humidity than the 95 %rh maintained in the chamber.)

Measurements of specimen mass are performed (perhaps once every 24 hours), until approximately six consecutive changes in mass (corrected for variation in the dummy), plotted versus time, fall “on a reasonably straight line” [952-1 clause 6.11.4.2.3]. The slope of this line (equal to rate of mass change, in grams per hour) is converted to WVT in grams per square metre per 24 hours [952-1 clause 6.11.5], using the measured area of the mouth of each dish. The mean of the WVT values of the three specimens is reported to the customer.

Here is a data set, for use in our discussion below:

Time	Dummy		Specimen 1			Specimen 2			Specimen 3
(h)	m (g)	dm (g)	m (g)	dm (g)	dm_corr (g)	m (g)	dm (g)	dm_corr (g)	m (g)	dm (g)	dm_corr (g)
0	163.4055	0.0000	197.6220	0.0000	0.0000	200.0488	0.0000	0.0000	190.0098	0.0000	0.0000
24	163.4061	0.0006	197.6260	0.0040	0.0034	200.0545	0.0057	0.0051	190.0167	0.0069	0.0063
48	163.4112	0.0057	197.6346	0.0126	0.0069	200.0615	0.0127	0.0070	190.0238	0.0140	0.0083
72	163.4148	0.0093	197.6408	0.0188	0.0095	200.0685	0.0197	0.0104	190.0326	0.0228	0.0135
120	163.4165	0.0110	197.6462	0.0242	0.0132	200.0753	0.0265	0.0155	190.0392	0.0294	0.0184
144	163.4182	0.0127	197.6554	0.0334	0.0207	200.0847	0.0359	0.0232	190.0471	0.0373	0.0246
Fitted slope (g/h):					0.000130			0.000145			0.000158
Area (mm^2):					3117			3117			3117
WVT (g/m^2/24h):					1.00			1.12			1.21

The slopes above were fitted using the LINEST spreadsheet function. Using the formula =LINEST(measured_y_values, measured_x_values, intercept, stats), with intercept=TRUE (allowing a non-zero y-intercept) and stats=TRUE (displaying not just the fitted values of slope and intercept, but also four additional rows of statistical information), for specimen 1, the following output is obtained:

0.000 130	0.000 11
0.000 013	0.001 09
0.963	0.001 59
103.10	4
0.000 26	0.000 01

The first row gives fitted slope and y-intercept, the second row standard errors (uncertainties at coverage factor k=1) of the fitted slope and intercept, the third row correlation coefficient R^2 and standard error in the y-values, the fourth row the Fisher F-statistic and the degrees of freedom (number of data points minus number of fitted parameters). We will discuss the use of some of these statistical measures below. (The fifth row is not of interest to this discussion.)

How may we estimate the uncertainty of measurement (UoM) of this WVT value? First, consider that the basic task is to determine the change in mass over the change in time, or $\displaystyle slope = \frac{\delta m}{\delta t}$ . The absolute accuracy of the balance used to weigh the dishes is not important, nor are the absolute times indicated by the watch: only the changes are of interest.

How can we estimate the accuracy of $\displaystyle \delta m$ ? We could evaluate the sensitivity of the balance [OIML R 76-1 clause T.4.1] to small changes in a load around 200 g (in the above example). However, there is an easier way, which also takes into account any effects that vary randomly from one balance reading to the next. As we have six data points to determine only two unknowns (slope and y-intercept of the straight line), we have what is called an “over-determined system”, for which we find the “best fit” line by the method of least squares. This line typically does not pass through any of the data points, but is “as close as possible” to all (in other words, the best compromise to all available data). The differences between the measured data points and the fitted line give a quantitative estimate of random errors in the measured values. These differences are conveniently combined in the standard error of the fitted slope, namely, 0.000 013 g/h for specimen 1 above. How do we expand this standard (k=1) uncertainty, to reach a level of confidence of approximately 95%? For a very large data set, we would simply multiply u(k=1) by the coverage factor k=2. However, as our data set is small, we should enlarge the coverage factor somewhat, to compensate for our limited knowledge. The t-distribution of Student tells us what this k-value should be: the spreadsheet function =TINV(1-0.95, 4) gives the value of Student’s t-distribution for 4 degrees of freedom and 95% level of confidence, namely, 2.8. Multiplying u(k=1) = 0.000 013 g/h by 2.8, we obtain the expanded uncertainty 0.000 036 g/h. (This is what U(k=2) would have been, if we had a very large data set, or, in other words, almost infinite degreees of freedom.) So, the slope for specimen 1 is (0.000 130 ± 0.000 036) g/h. Or, as a relative uncertainty, $\displaystyle \frac{U_{slope}}{slope} = \frac{0.000 036 g/h}{0.000 130 g/h} = 0.27$ , or 27%. Note that this is significantly worse than the balance sensitivity of 1% of total mass gain (which would translate to 0.000 001 g/h) required in the test methods [E96 clause 6.3, 952-1 clause 6.11.4.2.2], indicating that balance sensitivity is, in this case, negligible compared to other factors causing “noise” in the mass readings. It highlights the importance of having more data points than unknowns and performing a least squares fit, as this uncertainty component would otherwise be grossly underestimated. It also shows how the standard error in the slope is far more useful than the correlation coefficient R^2, in quantifying uncertainties.

Now, how do we estimate the uncertainty in $\displaystyle \delta t$ ? (In the previous paragraph, it seems we already obtained a “complete” uncertainty for the slope. However, the fitting procedure we used assumes no uncertainty in the x-values, only uncertainty in the y-values, so we had better look at the uncertainty in the time intervals, too.) The documentary standards require time intervals to be measured to an accuracy of 1% (for example, a 24 hour interval to an accuracy of 15 minutes), so, $\displaystyle \frac{U_{interval}}{interval} = 0.01$ [E96 clause 11.3, 952-1 clause 6.11.4.2.2]. We can see that the relative uncertainty in $\displaystyle \delta t$ is far smaller than that in the fitted slope, so we expect the uncertainty in slope to completely dominate the final, combined, uncertainty.

The formula for WVT is $\displaystyle WVT = \frac{slope}{area} * 24$ . When parameters are combined by simple multiplication or division, the relative uncertainties may be added simply in quadrature. So, $\displaystyle \frac{U_{WVT}}{WVT} = \sqrt{\left( \frac{U_{slope}}{slope} \right)^2 + \left( \frac{U_{interval}}{interval} \right)^2 + \left( \frac{U_{area}}{area} \right)^2 }$ . As $\displaystyle \frac{U_{area}}{area}$ is typically smaller than 0.01, it, like $\displaystyle \frac{U_{interval}}{interval}$ , can be neglected, so that the final relative uncertainty is $\displaystyle \frac{U_{WVT}}{WVT} = 0.27$ , or 27%. In other words, U(k=2) = 1.00 g/m^2/24h * 0.27 = 0.27 g/m^2/24h.

The above is the UoM for specimen 1. Specimens 2 and 3 have similar uncertainties (0.29 g/m^2/24h and 0.25 g/m^2/24h, respectively). Now, what is the uncertainty of the mean of the three specimens? If the three uncertainties are similar in magnitude, the uncertainty of the mean is $\displaystyle U_{mean} = \frac{U_i}{\sqrt{n}} = \frac{U_i}{\sqrt{3}} \approx \frac{0.27 \mathrm{g/m^2/24h}}{\sqrt{3}} = 0.16 \mathrm{g/m^2/24h}$ . If the uncertainties are quite different, the weighted mean (giving more weight to those specimens with smaller uncertainties) could be used: $\displaystyle \mathrm{weightedmean} = \frac{\sum{\frac{WVT_i}{{U_i}^2}}}{\sum{\frac{1}{{U_i}^2}}}$ . The uncertainty of the weighted mean is $\displaystyle \sqrt{\frac{1}{\sum{\frac{1}{{U_i}^2}}}}$ , which also works out to be 0.16 g/m^2/24h, in the above example.

Calibrating a platinum resistance thermometer at a fixed point

September 22, 2014 Hans Liedberg 2 Comments

The topic of this article is the determination of the resistance ratio, $\displaystyle W(t) = \frac{R(t)}{R_{tp}}$ , of a platinum resistance thermometer (PRT) at a thermometric fixed point, such as the freezing point of zinc ( $\displaystyle t = 419.527 \ ^{\circ} \mathrm{C}$ , on the ITS-90 temperature scale). It will discuss the data that should be recorded, the analysis of that data and the estimation of the Uncertainty of Measurement (UoM).

The design of fixed point cells and procedures to realise the required phase transitions are described elsewhere (for example, in Supplementary Information for the ITS-90, also called “the Red Book”). Likewise, using values of 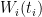$\displaystyle W_i(t_i)$ at several temperatures 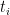$\displaystyle t_i$ , together with their uncertainties, 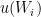$\displaystyle u(W_i)$ , to calculate ITS-90 deviation function coefficients and propagate uncertainty, is covered in papers such as MSL Technical Guide 21 – Using SPRT Calibration Certificates. Here, we only discuss data needed to determine 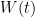$\displaystyle W(t)$ and to estimate 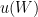$\displaystyle u(W)$ for one fixed point temperature.

The quantity to be determined is resistance ratio: this is the ratio of the PRT’s resistance at the fixed point temperature 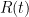$\displaystyle t$ , $\displaystyle R(t)$ , to that at the triple point of water (0.01 °C), $\displaystyle R_{tp}$ .

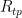Often, more than one PRT will be measured during the melt and freeze plateaus. One PRT must be measured repeatedly, to evaluate certain uncertainty components. We will call this “PRT1″, and the others, “additional PRTs”.

DATA TO BE RECORDED:

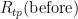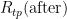1. For each PRT, $\displaystyle R_{tp}(\mathrm{before})$ and $\displaystyle R_{tp}(\mathrm{after})$ the measurement at the fixed point.

Notes:

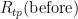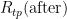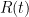a) All three of the resistances, $\displaystyle R_{tp}(\mathrm{before})$ , $\displaystyle R_{tp}(\mathrm{after})$ and $\displaystyle R(t)$ , should be measured using the same resistance measuring instrument, on the same range. If it is a bridge, the same standard resistor should be used, too. This is so that two uncertainty components, calibration uncertainty of the standard resistor, and errors in range amplifiers or attenuators, cancel out in the ratio, and only non-linearity of the measuring instrument remains.

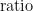b) If a bridge is used with the same standard resistor, bridge ratios may be recorded in place of resistances. Since the standard resistor value, $\displaystyle R_s$ , is constant (except for its temperature variation, considered in the uncertainty analysis, later), using $\displaystyle R_x = \mathrm{ratio} \cdot R_s$ , or just $\displaystyle \mathrm{ratio}$ , will give the same resistance ratio. This applies for all resistance records mentioned below, except when noted otherwise.

c) Don’t confuse “bridge ratio”, 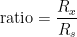$\displaystyle \mathrm{ratio} = \frac{R_x}{R_s}$ , and “resistance ratio”, $\displaystyle W = \frac{R_x}{R_{tp}}$ .

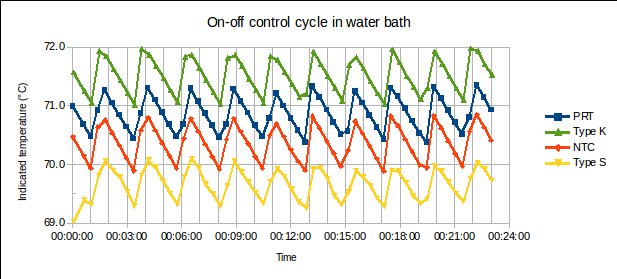
2. Furnace or bath setpoints used for melt, supercool, and freeze. This is so that we can change these setpoint temperatures next time, to achieve longer plateaus. Note: Do not make the setpoints so close to the fixed point temperature that stable furnace control may be mistaken for a plateau. Also, ensure that temperature variation does not take the furnace below the melting temperature at certain points during the control cycle (during the melt), or above the freezing temperature (during the freeze). Rather sacrifice some plateau time, and get unambiguous plateaus.

3. Melt:

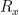(Note: The y-axes of the graphs below are graduated in temperature units, for convenient visual interpretation. Readings could, equivalently, have been plotted as resistance ratios $\displaystyle W$ , resistances $\displaystyle R_x$ , or bridge ratios.)

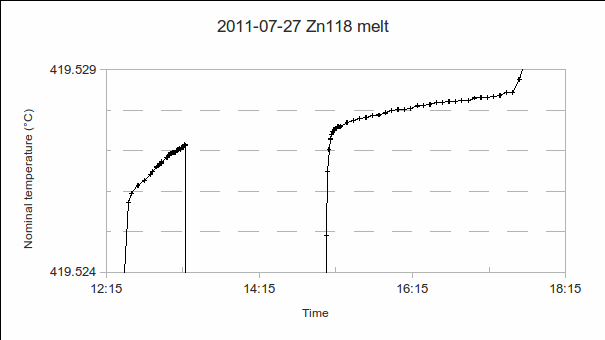
a) Start time: This may be determined after completing the measurement, by studying a graph of PRT1’s readings. (In the example above, it’s 12:35.)

b) PRT1’s resistance at the solidus (start of the melt): This is needed to determine the melting range, that is, the difference from the liquidus (at the end of the melt). (In the example above, it’s 419.526 °C.)

c) End time: As for start time. (In the example above, it’s 17:35, in other words, the melt lasted five hours.)

d) PRT1’s resistance at the liquidus (end of the melt): Additional PRTs may be calibrated during the melt (as in the above example, from 13:20 to 15:00), but the end of the melt should be recorded using PRT1, so that the melting range and melt-freeze coincidence can be accurately determined. (In the example above, it’s 419.528 4 °C. In other words, the melting range is 0.002 4 °C.)

4. “Soak”, when the fixed point material is in the liquid state for several hours, after the melt:

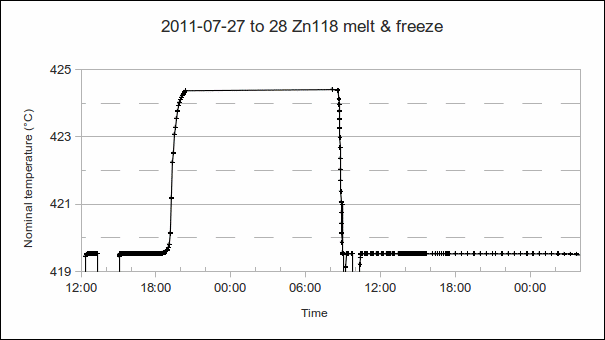
a) PRT1’s resistance, when the temperature has stabilised: Calculate the approximate difference from the melt temperature. (The approximate PRT sensitivity, 0.1 Ω/°C or 0.39 Ω/°C, may be used to convert differences in ohms to °C.) Use this to determine the offset (or error, or correction) of the furnace or bath’s temperature controller. This allows better setpoints to be used next time, more closely approaching the “melt + 5 °C” and “freeze – 1 °C” furnace temperatures commonly desired during melt and freeze. (In the example above, the “soak” temperature is approximately 5 °C above the melt, as desired.)

5. Supercool:

a)Time that the setpoint is reduced: This will tell us how long it takes for recalescence to occur. (If it takes too long, the chosen setpoint may be lower next time.)

b) Setpoint used during the supercool: This is usually several °C lower than that during the freeze, to hasten recalescence and the start of the freeze.

c) Time at which recalescence occurs: See a).

d) PRT1’s resistance, at the moment of recalescence: When the liquid starts solidifying, the temperature starts rising out of the supercool. The depth of the supercool (difference from freeze temperature) gives a rough indication of the “condition” (purity?) of the fixed point cell material. (The more impurities, the more easily nucleation occurs and freezing starts, therefore the shallower the supercool.)

(In the example above, the setpoint was reduced at 8:35, the PRT reached a minimum reading of 419.521 °C, and recalescence occurred at 9:00.)

6. Freeze:

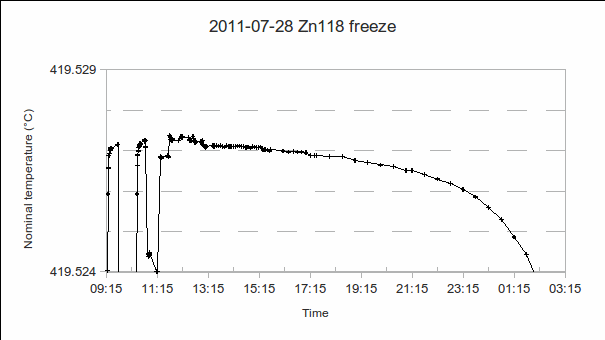
a) Start time.

b) PRT1’s resistance at the liquidus (start of the freeze): If plateau shapes are as expected (PRT reading rising as the melt progresses, and falling as the freeze progresses), the melt-freeze coincidence is calculated as 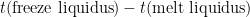$\displaystyle t(\mathrm{freeze \ liquidus}) - t(\mathrm{melt \ liquidus})$ . As the furnace temperature is several °C colder during freeze than melt, this difference in PRT readings indicates the sensitivity (if any) of the PRT to the environment outside the fixed point cell.

(In the above example, PRT1 reads 419.527 1 °C from 9:25 to 9:45, then an additional PRT is calibrated from 9:45 to 10:20, and PRT1 reads 419.527 2 °C from 10:30 to 10:45. Freeze – melt = 419.527 2 °C – 419.528 4 °C = -0.001 2 °C.)

c) Self-heating of the PRT: If the resistance measuring instrument allows it, change the current passing through the PRT (preferably by a factor of √2 or 1/√2, so that the power dissipated in the resistance element is conveniently doubled or halved) and note the change in its resistance. (These readings are not shown in the graph above.)

d) Vertical temperature gradients in the cell, during the plateau: These should preferably be evaluated during the plateau where the furnace or bath provides least compensation for stem conduction errors, that is, the freeze, for fixed points above room temperature, or the melt, for fixed points below room temperature.

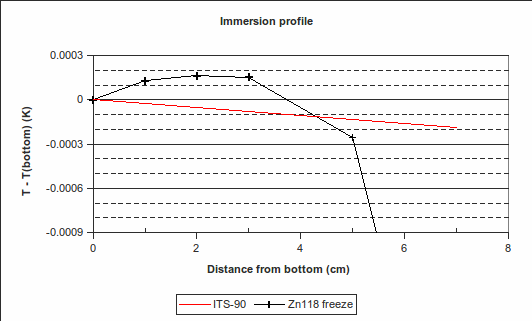
(In the above example, PRT1’s immersion was changed to 70 mm, 50 mm, 30 mm, 20 mm and 10 mm above the bottom of the re-entrant well, from 10:50 to 13:00. Its readings were 419.524 °C, 419.526 8 °C, 419.527 3 °C, 419.527 3 °C and 419.527 2 °C, respectively. Its reading back at maximum immersion was 419.527 1 °C, very close to the value at the start of the freeze, indicating that the zinc cell was still on the freeze plateau. The red “ITS-90″ line in the immersion profile above is the expected variation in freezing temperature caused by a change in depth, according to the hydrostatic head coefficient for zinc published in the ITS-90 Table 2.)

Regarding the sequence of immersion depths: PRT1 is first raised to the highest position, then lowered, step-by-step, back down again. This is because raising the PRT causes some cold air to enter the re-entrant well, temporarily cooling the PRT. To avoid a resulting error, all but one of the measurements are done while increasing the immersion depth.

e) End time.

f) PRT1’s resistance at the solidus (end of the freeze): Additional PRTs may be calibrated during the freeze, but PRT1 should be re-inserted before the end of the freeze, so that the freezing range can be determined. In order to know what time period is available to calibrate other PRTs, record the first melt and freeze (using this combination of fixed point cell and furnace) using just one PRT. Note: If additional PRTs are to be inserted in the fixed point cell, they should be pre-heated (or cooled) to approximately the fixed point temperature, before insertion, to avoid excessive shortening of the freeze plateau.

(As can be seen in the above example, rounding of the plateau makes it difficult to precisely locate the end of the freeze. However, it is the temperature stability during the measurements from 9:25 to 13:00, when additional PRTs, self-heating and immersion measurements were performed, that is most important. The shape of the rest of the plateau is useful as an indicator of furnace temperature uniformity, and, consequently, shape of the solid-liquid interface, as the phase transition progresses, but will not be used in the uncertainty analysis. So, somewhat arbitrarily, the end of the freeze is estimated as 23:15, 419.526 °C, giving a freezing range of about 0.001 °C and a 14-hour freeze plateau.)

DETERMINING THE RESISTANCE RATIO $\displaystyle W(\mathrm{Zn})$ :

The liquidus temperature, when almost all the material is liquid (at the end of the melt or the start of the freeze), is closest to the ideal phase transition temperature [McLaren, “The freezing points of high purity metals as precision temperature standards”, In Temperature: Its Measurement and Control in Science and Industry, Vol. 3, 1962, 185-198]. For all but one of the metal fixed points used to calibrate PRTs (mercury, indium, …, silver), the freeze is usually preferred over the melt. (Gallium is used on the melt, as it has such a large supercool that its freeze cannot be used.) So, for $\displaystyle R(\mathrm{Zn})$ we will use the value at the start of the freeze (the resistance equivalent to 419.527 2 °C), namely, 65.619 14 Ω.

The phase transition temperature published in the ITS-90 is that at the surface of the fixed point material. The temperature changes with increasing depth, due to the increasing pressure exerted by the column of material above the measurement location. For zinc, this hydrostatic head effect is 2.7 mK/m (“depth” coefficient in ITS-90 Table 2). The mid-point of the PRT sensing element is 155 mm below the surface of the zinc, where it is 0.002 7 °C/m x 0.155 m = 0.000 4 °C hotter than at the surface. The resistance corrected for hydrostatic head is therefore 65.619 14 Ω – 0.000 4 °C x 0.1 Ω/°C = 65.619 10 Ω.

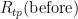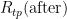For $\displaystyle R_{tp}(\mathrm{before})$ and $\displaystyle R_{tp}(\mathrm{after})$ , the measured values are 25.547 308 Ω and 25.547 304 Ω, respectively. The hydrostatic head effect in the WTP cell is -0.73 mK/m x 0.265 m = -0.000 19 °C. (Note the difference in sign from zinc: water, unusually, freezes at a lower temperature when the pressure increases.) The resistances corrected for hydrostatic head are 25.547 327 Ω and 25.547 323 Ω, respectively.

The zinc cell was sealed by the manufacturer, with the gas pressure adjusted to be 101.3 kPa at the freezing temperature, so no correction is required for gas pressure. (The phase transition temperature varies with varying gas pressure above the fixed point material, according to the “pressure” coefficient published in ITS-90 Table 2.) The water cell, being a triple point, should not contain any gas but water vapour, so no gas pressure correction is applied here, either.

So, 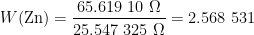$\displaystyle W(\mathrm{Zn}) = \frac{65.619 \ 10 \ \Omega}{25.547 \ 325 \ \Omega} = 2.568 \ 531$ .

The resistances were measured at 1 mA current. (It is common practice to correct fixed point calibration data to 0 mA current, using the self-heating measurements mentioned above. However, here we do not correct for self-heating, as we plan to use the PRT at 1 mA current without applying self-heating corrections. For interest’s sake, the self-heating of this PRT due to the 1 mA current was 0.000 08 Ω at the zinc point and 0.000 02 Ω at the water triple point: these values are very small, owing to the design of this model of PRT.)

COMPONENTS OF MEASUREMENT UNCERTAINTY [CCT-WG3, “Uncertainties in the realisation of the SPRT subranges of the ITS-90″, CCT/08-19/rev]:

1. Gas pressure: The uncertainty in gas pressure inside a sealed fixed point cell may be estimated as 3 kPa (coverage factor k=1), if no method of measuring it exists [CCT-WG3 guide, section 2.1]. To convert to temperature units, use the gas pressure coefficient of 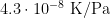$\displaystyle 4.3 \cdot 10^{-8} \ \mathrm{K/Pa}$ for zinc [ITS-90 Table 2], yielding 0.000 1 °C (k=1). For the WTP cell, the residual gas pressure may be estimated by the inverting the cell and observing how much the remaining gas bubble is compressed [CCT-WG3 guide, section 3.1]: observing a reduction in bubble volume of 100 times, we estimate the effect of the residual gas pressure as 0.000 002 °C (k=1).

2. Hydrostatic pressure: We estimate the uncertainty in immersion depth of the mid-point of the PRT element below the surface of the zinc or water to be 10 mm (k=1). (This uncertainty arises from lack of knowledge of the exact depth of the zinc, as well as thermal expansion inside the fixed point cell and the PRT as the temperature rises.) For zinc, 2.7 mK/m x 0.01 m = 0.000 03 °C (k=1). For the WTP, -0.73 mK/m x 0.01 m = 0.000 007 °C (k=1).

3. Chemical impurities and isotopic composition: Earlier, we mentioned that the liquidus temperature is closest to the ideal phase transition temperature, and chose to use the value at the start of the freeze. The liquidus temperature differs from the ideal temperature because the fixed point material is not completely pure. The zinc cell manufacturer reported the total mole fraction of impurities to be 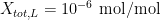$\displaystyle X_{tot,L} = 10^{-6} \ \mathrm{mol/mol}$ . Using this information, the uncertainty in the liquidus temperature may be estimated using the “overall maximum estimate” (OME) method: 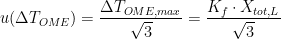$\displaystyle u(\Delta T_{OME}) = \frac{\Delta T_{OME,max}}{\sqrt{3}} = \frac{K_f \cdot X_{tot,L}}{\sqrt{3}}$ , where the cryoscopic constant $\displaystyle K_f = 564 \ \mathrm{K}$ for zinc, so that $\displaystyle u(\Delta T_{OME}) = \frac{10^{-6} \cdot 564 \ \mathrm{K}}{\sqrt{3}} = 0.000 \ 3 \ \mathrm{K}$ (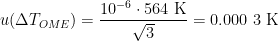k=1) [CCT-WG3 guide, equation (2.23) and Appendix B]. (The melting range following a slow freeze was previously recommended as an indicator of purity: the purer the material, the narrower the melting range. However, some significant impurities may not betray their presence by an increased melting range, so this range is only used for quality assurance purposes now, to indicate changes in the cell or furnace condition.) For the WTP cell, we have no impurity information, so we use a literature value of 0.000 05 °C (k=1.732) [CCT-WG3 guide, section 3.2]. Likewise, for the isotopic composition of the water, we use a literature value of 0.000 1 °C (k=1.732) [CCT-WG3 guide, section 3.3].

4. Immersion and thermal effects: The vertical temperature gradient measured during the zinc freeze deviates from the expected behaviour by a maximum of 0.000 25 °C over the bottom 30 mm, with the PRT being hotter than expected. (See the difference between the “Zn118 freeze” line and the red “ITS-90″ line in the “Immersion profile” graph above. We choose 30 mm as it is approximately half the length of the PRT element.) However, 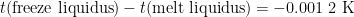$\displaystyle t(\mathrm{freeze \ liquidus}) - t(\mathrm{melt \ liquidus}) = -0.001 \ 2 \ \mathrm{K}$ , suggesting that the lower furnace temperature during the freeze causes the PRT to be colder than expected during that plateau. To be conservative, we will use the larger of these values, 0.001 2 °C (k=1.732), as the uncertainty due to immersion and thermal effects for zinc. For the WTP, the following immersion profile was measured:

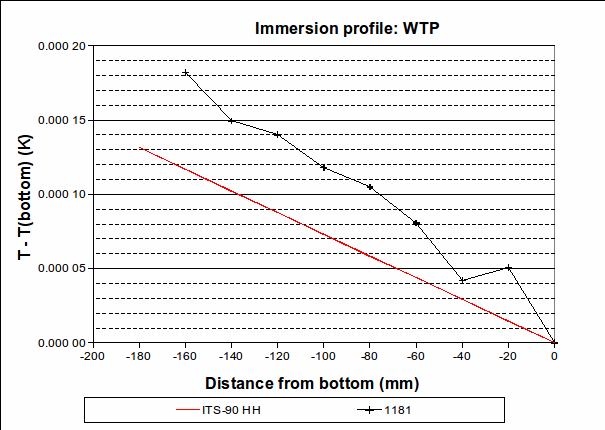
The largest deviation from the expected profile, over the bottom 30 mm, is 0.000 036 °C. We use this value as the half-width of a rectangular distribution (k=1.732).

5. Difference from the liquidus point: PRT1 was measured at the end of the melt and at the start of the freeze, that is, at the liquidus point. However, the additional PRTs measured during the melt were 0.001 3 °C to 0.000 8 °C below the liquidus point. (See the melt graph of PRT1, above.) So, the additional PRTs measured during the melt must include an additional uncertainty component of approximately 0.001 °C (k=1.732?) to account for this difference. The one measured during the freeze was at the liquidus point (considering the agreement of PRT1’s readings before and after).

6. PRT oxidation state, crystal defects and strain (variation in 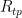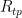$\displaystyle R_{tp}$ ): $\displaystyle R_{tp}$ changes somewhat during the fixed point measurement, because of various causes. The uncertainty component associated with this variation is 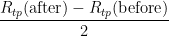$\displaystyle \frac{R_{tp}(\mathrm{after}) - R_{tp}(\mathrm{before})}{2}$ , which is 0.000 02 °C (k=1.732) in temperature units. The effect of variation in 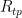$\displaystyle R_{tp}$ is larger, the higher the temperature: the uncertainty scales according to W(t).

7. Self-heating: We do not correct measured resistances at 1 mA to zero current, therefore we do not include an uncertainty for self-heating.

8. Resistance measuring instrument – non-linearity: The bridge non-linearity has been evaluated as 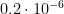$\displaystyle 0.2 \cdot 10^{-6}$ (k=2) in units of bridge ratio. To find the uncertainty in 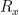$\displaystyle R_x$ , multiply by $\displaystyle R_s$ , which is 100 Ω, yielding 0.000 02 Ω. Dividing by 0.1 Ω/°C, we obtain 0.000 2 °C (k=2).

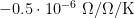9. Standard resistor: The temperature coefficient of $\displaystyle R_s$ is $\displaystyle -0.5 \cdot 10^{-6} \ \Omega / \Omega / \mathrm{K}$ . The maximum variation in its temperature during the measurements is estimated to be 0.2 °C (k=1.732), yielding an uncertainty in 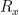$\displaystyle R_x$ of $\displaystyle -0.5 \ \cdot 10^{-6} \ \Omega / \Omega / \mathrm{K} \cdot 0.2 \ \mathrm{K} \cdot 65.619 \ \Omega = 0.000 \ 007 \ \Omega$ , or 0.000 07 °C (k=1.732).

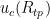We want to calculate the uncertainty in resistance ratio $\displaystyle W(t) = \frac{R(t)}{R_{tp}}$ . To do this, we first calculate $\displaystyle u_c(R_{tp})$ , propagate that to the zinc temperature by multiplying by W(Zn), then combine it with the other components relevant to the zinc point. In doing this, beware of double-counting components: Variation in 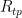$\displaystyle R_{tp}$ must be included in the WTP budget (as is), or in the Zn budget (scaled by W(Zn) = 2.569), but not in both. Bridge non-linearity affects the ratio between Zn and WTP readings more than it does the very narrowly varying 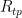$\displaystyle R_{tp}$ value, so we only count it once, in the Zn budget. 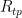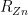Variation in the temperature of the standard resistor was estimated over the day or so between measurements of $\displaystyle R_{tp}$ and $\displaystyle R_{Zn}$ , so is also only counted once.

WTP uncertainty budget:

Component	Value (mK)	Divisor	Sensitivity coeff	u(k=1) (mK)
Gas pressure	0.002	1	1	0.002
Hydrostatic head	0.007	1	1	0.007
Impurities	0.05	1.732	1	0.029
Isotopic composition	0.1	1.732	1	0.058
Immersion	0.036	1.732	1	0.021
Difference from liquidus
Variation in Rtp
Self-heating
Bridge non-linearity
Std resistor
Propagation of u(Rtp)
uc(k=1)				0.062

Zn uncertainty budget:

Component	Value (mK)	Divisor	Sensitivity coeff	u(k=1) (mK)
Gas pressure	0.1	1	1	0.1
Hydrostatic head	0.03	1	1	0.03
Impurities	0.3	1	1	0.3
Isotopic composition
Immersion	1.2	1.732	1	0.7
Difference from liquidus	0	1.732	1	0
Variation in Rtp	0.02	1.732	2.569	0.01
Self-heating
Bridge non-linearity	0.2	2	1	0.1
Std resistor	0.07	1.732	1	0.04
Propagation of u(Rtp)	0.062	1	2.569	0.16
uc(k=1)				0.8

The dominant component in the Zn budget is immersion (stem conduction error). As we were very conservative in estimating this component (the value from the immersion profile measurement was five times smaller than the freeze-melt value used), we can safely assume large degrees of freedom in this component, therefore large effective degrees of freedom in the combined uncertainty. So, we multiply by a coverage factor of k=2 to obtain the expanded uncertainty $\displaystyle \mathrm{U}(W_{\mathrm{Zn}}) = 0.001 \ 6 \ \mathrm{K}$ . (Actually, as the dominant component follows a rectangular distribution, we’re entitled to use k=1.65 [EA-4/02 M: 1999, Expression of the Uncertainty of Measurement in Calibration, section S9.14], yielding 0.001 3 K, but let’s be conservative and stick with 1.6 mK.)

(Contact the author at lmc-solutions.co.za.)

Uncertainty of measurement: relative humidity via dew point and air temperature

September 16, 2014 Hans Liedberg 2 Comments

This article discusses the calibration of a relative humidity (RH) hygrometer by comparison with a condensation (“chilled mirror”) dewpoint hygrometer and a thermometer measuring air temperature (“dry-bulb temperature”, in humidity parlance). It focuses on estimation of the uncertainty to be associated with the measurement result.
The comparison between the RH hygrometer (Unit Under Test, or UUT) and the dewpoint hygrometer and thermometer (together forming the reference standard) is performed in a temperature- and humidity-variable chamber. The dewpoint hygrometer measures dew-point (or frost-point, if below 0 °C) temperature, $\displaystyle t_d$ , with an uncertainty of 0.1 °C (coverage factor k=2). A resistance thermometer is used to measure the air temperature, $\displaystyle t$ , also with an uncertainty of 0.1 °C (k=2). (No correction is applied for self-heating of the resistance thermometer, as it was calibrated in air, that is, in similar conditions to those in which it is used.) The temperature uniformity of the chamber is specified by the manufacturer to be ± 0.3 °C. (We assume a coverage factor of k = √3.)
Measurements are performed at temperatures of 5 °C, 20 °C and 50 °C, and at relative humidities of 10 %rh, 50 %rh and 90 %rh.

First, we must be able to calculate relative humidity from measured values of dew point and air temperature. Relative humidity is defined as a ratio of water vapour pressures: $\displaystyle RH = \frac{e}{e_s}$ , where $\displaystyle e$ is the actual vapour pressure of water and $\displaystyle e_s$ is the saturation vapour pressure of water at the prevailing temperature [Beginner’s guide to humidity measurement, NPL Good Practice Guide No 124, p 17]. (Here we express RH from 0 to 1, not 0 %rh to 100 %rh.) We will use the Magnus formula to calculate water vapour pressures: $\displaystyle e_s = 611.2 \ \mathrm{Pa} \cdot exp^{a \cdot t/(b + t)}$ , where $\displaystyle e_s$ is saturation water vapour pressure (in Pa) at temperature $\displaystyle t$ (in °C), $\displaystyle exp$ is used for the irrational number 2.718… (to distinguish it from the symbol for vapour pressure), and the constants are $\displaystyle a = \begin{cases} 17.62, & \text{if } t \ge 0 ^{\circ} \text{C} \\ 22.46, & \text{if }t < 0 ^{\circ} \text{C} \end{cases}$ and $\displaystyle b = \begin{cases} 243.12, & \text{if } t \ge 0 ^{\circ} \text{C} \\ 272.62, & \text{if }t < 0 ^{\circ} \text{C} \end{cases}$ [Guide to the measurement of humidity, Institute of Measurement and Control, 1996, p 53]. The Magnus formula has an uncertainty of less than 1.0 % (k=2) from -65 °C to 60 °C. We will not apply the water vapour enhancement factor to $\displaystyle e$ or $\displaystyle e_s$ , to account for the presence of gases other than water vapour, as it would cancel in the ratio $\displaystyle RH = \frac{e}{e_s}$ .

How do we determine the actual water vapour pressure, $\displaystyle e$ ? It is the saturation water vapour pressure at the dew-point temperature $\displaystyle t_d$ , by the definition of dew point [Beginner’s guide to humidity measurement, p 2]. So, applying the Magnus formula, $\displaystyle e = 611.2 \ \mathrm{Pa} \cdot exp^{a \cdot t_d/(b + t_d)}$ .

We may also need to calculate dew point from relative humidity and air temperature. To achieve this, first calculate vapour pressure $\displaystyle e = RH \cdot e_s(t)$ , then manipulate the Magnus formula to obtain $\displaystyle t_d = \frac{b \cdot ln(e/611.2 \ \mathrm{Pa})}{a - ln(e/611.2 \ \mathrm{Pa})}$ [Guide to the measurement of humidity, Institute of Measurement and Control, 1996, p 54].

We will also need the sensitivity coefficients $\displaystyle \frac{\partial RH}{\partial t_d}$ and $\displaystyle \frac{\partial RH}{\partial t}$ :

$\displaystyle \frac{\partial RH}{\partial t_d} = \frac{\partial RH}{\partial e} \frac{\partial e}{\partial t_d} = \frac{RH}{e} \cdot e \cdot \frac{a \cdot b}{(b+t_d)^2} = RH \cdot \frac{a \cdot b}{(b+t_d)^2}$ $\displaystyle \frac{\partial RH}{\partial t} = \frac{\partial RH}{\partial e_s} \frac{\partial e_s}{\partial t} = \frac{-RH}{e_s} \cdot e_s \cdot \frac{a \cdot b}{(b+t)^2} = -RH \cdot \frac{a \cdot b}{(b+t)^2}$

Evaluating the sensitivities at typical temperatures $\displaystyle t_d$ = -20 °Cfp to 50 °Cdp and $\displaystyle t$ = 5 °C to 50 °C, we see the familiar rule-of-thumb that $\displaystyle \frac{\partial RH}{\partial t_d} \approx 0.06 \ \mathrm{RH}$ or $\displaystyle \frac{\partial RH}{\partial t} \approx -0.06 \ \mathrm{RH}$ , in other words, RH changes by approximately 6% of the value, for a change of 1 °C in dew point or air temperature. (The symbols °Cfp and °Cdp, for “degrees Celsius frostpoint” and “degrees Celsius dewpoint”, are commonly used to distinguish dew-point temperature, a measure of humidity, from air temperature.) In other words, if $\displaystyle t_d$ increases from 8 °Cdp to 9 °Cdp (at $\displaystyle t$ = 20 °C), RH changes from 0.46 (or 46 %rh) to 0.49 (or 49 %rh), an increase of 3 %rh, or 6% of value. If $\displaystyle t$ increases from 49 °C to 50 °C (at $\displaystyle t_d$ = 48 °Cdp), RH changes from 0.95 (95 %rh) to 0.90 (90 %rh), a decrease of 5 %rh, or 6% of value.

Here are the dew points, for the air temperature and relative humidity measurement points mentioned above:

	Air temp: 5 °C	20 °C	50 °C
RH: 10 %rh	-21.8 °Cfp	-11.2 °Cfp	10.1 °Cdp
50 %rh	-4.0 °Cfp	9.3 °Cdp	36.7 °Cdp
90 %rh	3.5 °Cdp	18.3 °Cdp	47.9 °Cdp

We will evaluate uncertainties for the three combinations indicated in bold in the table above.

We estimate hysteresis of the UUT, a capacitive RH sensor, to vary from zero at 10 %rh to 0.6 %rh (k=1) at 50 %rh to zero at 90 %rh.

5 °C, RH = 0.10 (10 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	-21.8 °Cfp	0.05 °C	0.010	0.0005
Air temperature	5.0 °C	0.05 °C	-0.007	-0.0004
Chamber: Temperature gradient		0.17 °C	-0.007	-0.0012
UUT: Hysteresis		0.000 RH	1	0.0000
Combined uncertainty (k=1)				0.0013
U(k=2)				0.003 (0.3 %rh)

20 °C, RH = 0.50 (50 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	9.3 °Cdp	0.05 °C	0.034	0.0017
Air temperature	20.0 °C	0.05 °C	-0.031	-0.0015
Chamber: Temperature gradient		0.17 °C	-0.031	-0.0054
UUT: Hysteresis		0.006 RH	1	0.0060
Combined uncertainty (k=1)				0.0083
U(k=2)				0.017 (1.7 %rh)

50 °C, RH = 0.90 (90 %rh):

Component	Value	u(k=1)	Sensitivity	u(RH)
Ref std: Dewpoint	47.9 °Cdp	0.05 °C	0.046	0.0023
Air temperature	50.0 °C	0.05 °C	-0.045	-0.0022
Chamber: Temperature gradient		0.17 °C	-0.045	-0.0078
UUT: Hysteresis		0.000 RH	1	0.0000
Combined uncertainty (k=1)				0.0084
U(k=2)				0.017 (1.7 %rh)

(Contact the author at lmc-solutions.co.za.)

Uncertainty of measurement: conventional mass of a weight

September 13, 2014 Hans Liedberg Leave a comment

This article will discuss the calibration of a 1 kg weight of class $\displaystyle F_1$ by comparison with a 1 kg weight of class $\displaystyle E_2$ (weight classes are described in OIML R 111-1), using a balance of resolution 0.1 mg. In particular, it will focus on the estimation of uncertainty of measurement (UoM) for this calibration, for which the result is intended to be reported as a conventional mass (as discussed in OIML D 28).

The 80-page document R 111-1 describes many characteristics of weights (for example, construction) that are of limited relevance to the calibration laboratory: we will use mostly the sections on Maximum Permissible Errors (section 5, p 11-12), Density (sections 10, p 17-18 and B.7.9.3, p 58) and, especially, Calibration (Annex C, p 61-70). The 12-page document D 28, “Conventional value of the result of weighing in air”, presents a convenient summary of the information most relevant to calibration.

The conventional mass of a body is equal to the mass $\displaystyle m_c$ of a standard weight that balances this body under “conventional” conditions, namely, ambient temperature $\displaystyle t_{ref}$ = 20 °C, air density $\displaystyle \rho_0 = 1.2 \ \mathrm{kg.m^{-3}}$ and standard weight density $\displaystyle \rho_c = 8000 \ \mathrm{kg.m^{-3}}$ [D 28 section 4, p 5]. The conditions have been chosen such that mass, $\displaystyle m$ , and conventional mass, $\displaystyle m_c$ , of a weight do not differ “much” [D 28 section 0, p 4]. However, we will see, when we try to achieve the required calibration uncertainty for a 1 kg $\displaystyle F_1$ weight, which is $\displaystyle U(m_{ct}) \le \frac{\delta m}{3} = \frac{5 \ \mathrm{mg}}{3} = 1.7 \ \mathrm{mg}$ [R 111-1 section 5.2 and Table 1, p 11-12], or, equivalently, a relative standard uncertainty of $\displaystyle \frac{u_c(m_{ct})}{m_{ct}} \le 0.8 \cdot 10^{-6}$ , that typical deviations of weight density from the conventional $\displaystyle \rho_c = 8000 \ \mathrm{kg.m^{-3}}$ can cause significant differences between $\displaystyle m$ and $\displaystyle m_c$ .

Note: The subscript “c” indicates “conventional”, “r” refers to the reference weight (in other words, the measurement standard) and “t” refers to the test weight (or Unit Under Test).

The relation between conventional mass and mass is given by $\displaystyle m_c = m \frac{1-\rho_0 / \rho}{1-\rho_0 / \rho_c}$ [D 28 equation 1, p 6].

In our example, both the reference weight and the test weight are made of stainless steel. The mass of the reference weight is chosen to be $\displaystyle m_r = 1.000 \ 000 \ 00 \ \mathrm{kg}$ , with the largest calibration uncertainty allowed by R 111-1 for class $\displaystyle E_2$ weights. Relevant data are presented in the table below.

Quantity	Uncertainty	Reference
$\displaystyle m_r = 1.000 \ 000 \ 00 \ \mathrm{kg}$
$\displaystyle \rho_r = 7950 \ \mathrm{kg.m^{-3}}$	$\displaystyle u(\rho_r) = 70 \ \mathrm{kg.m^{-3}}$	[R 111-1 Table B.7, p 58]
$\displaystyle m_{cr} = m_r \frac{1-\rho_0 / \rho_r}{1-\rho_0 / \rho_c} = (1-0.94 \cdot 10^{-6}) \ \mathrm{kg}$	$\displaystyle u(m_{cr}) = \frac{\delta m (E_2)}{6} = 0.000 \ 000 \ 27 \ \mathrm{kg}$	[R 111-1 Table 1, p 12]
$\displaystyle \rho_t = 7950 \ \mathrm{kg.m^{-3}}$	$\displaystyle u(\rho_t) = 70 \ \mathrm{kg.m^{-3}}$	[R 111-1 Table B.7, p 58]
Air pressure $\displaystyle p = 750 \ \mathrm{mbar}$	$\displaystyle u(p) = 5 \ \mathrm{mbar}$
Humidity $\displaystyle hr = 50 \ \mathrm{\% rh}$	$\displaystyle u(hr) = 5 \ \mathrm{\% rh}$
Air temperature $\displaystyle t = 19.0 \ \mathrm{^{\circ}C}$	$\displaystyle u(t) = 0.5 \ \mathrm{^{\circ}C}$
$\displaystyle \rho_a = \frac{0.34848 \cdot p - 0.009 \cdot hr \cdot e^{0.061t}}{273.15+t}$ $\displaystyle = 0.890 \ \mathrm{kg.m^{-3}}$	$\displaystyle u(\rho_a) = 0.005 \ \mathrm{kg.m^{-3}}$ (see below for calculation)	[R 111-1 equation (E.3-1), p 76]

Notes:

1.The conventional mass $\displaystyle m_{cr}$ is $\displaystyle 0.94 \cdot 10^{-6}$ lower than $\displaystyle m_r$ : this difference is large (compared to the $\displaystyle 0.8 \cdot 10^{-6}$ relative uncertainty goal), although the assumed weight density is not far from ideal.

2. As the densities of the reference and test weights are not known, they are “assumed” according to R 111-1 Table B.7 (for stainless steel). Although they are assumed to be the same in most of the data analysis below, the possible difference between the densities must be taken into account in the uncertainty analysis. In particular, during calculation of the uncertainty in the air buoyancy correction $\displaystyle C$ , the sensitivity coefficient of $\displaystyle u(\rho_a)$ will be calculated using the worst-case scenario: as $\displaystyle 7810 \ \mathrm{kg.m^{-3}} \le \rho_r \le 8210 \ \mathrm{kg.m^{-3}}$ for 1 kg $\displaystyle E_2$ weights and $\displaystyle 7390 \ \mathrm{kg.m^{-3}} \le \rho_t \le 8730 \ \mathrm{kg.m^{-3}}$ for 1 kg $\displaystyle F_1$ weights [R 111-1 Table 5, p 17], the sensitivity coefficient $\displaystyle \left( \frac{1}{\rho_t} - \frac{1}{\rho_r} \right) = \left( \frac{1}{7390 \ \mathrm{kg.m^{-3}}} - \frac{1}{8210 \ \mathrm{kg.m^{-3}}} \right) = 14 \cdot 10^{-6} \mathrm{m^3.kg^{-1}}$ will be used. (The calculation is performed below.)

3. The air pressure $\displaystyle p$ , and, consequently, air density $\displaystyle \rho_a$ , are unusually low, because the measurements were performed at an altitude of 2400 m. The even-more-approximate formula for air density, $\displaystyle \rho_a = \rho_0 \cdot e^{-\rho_0 \cdot g \cdot h / p_0}$ [R 111-1 equation (E.3-2), p 76], yields a similar air density, $\displaystyle 0.91 \ \mathrm{kg.m^{-3}}$ .

The uncertainty in air density is calculated as follows: $\displaystyle u(\rho_a) = \sqrt{\left( \frac{\partial \rho_a}{\partial p} u(p)\right)^2 + \left( \frac{\partial \rho_a}{\partial hr} u(hr)\right)^2 + \left( \frac{\partial \rho_a}{\partial t} u(t)\right)^2} = \rho_a \sqrt{\left( 10^{-3} \mathrm{mbar}^{-1} \cdot u(p) \right)^2 + \left( -10^{-4} \cdot u(hr) \right)^2 + \left( -3.4 \cdot 10^{-3} \mathrm{K}^{-1} \cdot u(t) \right)^2}$ $\displaystyle = 0.890 \ \mathrm{kg.m^{-3}} \cdot \sqrt{0.0050^2 + 0.0005^2 + 0.0017^2} = 0.005 \ \mathrm{kg.m^{-3}}$ . Sensitivity coefficients come from R 111-1 section C.6.3.6 (p 68), with $\displaystyle \frac{\partial \rho_a}{\partial p}$ and $\displaystyle \frac{\partial \rho_a}{\partial hr}$ being converted from $\displaystyle \mathrm{Pa^{-1}}$ to $\displaystyle \mathrm{mbar^{-1}}$ and from fractional relative humidity to %rh, respectively. (Both change by a factor of 100, though in opposite directions.) It is clear that air pressure has the largest effect on air density, followed by temperature, with the effect of relative humidity being negligible.

The conventional masses of test and reference weights are related as follows:

$\displaystyle m_{ct} = m_{cr}(1+C) + \Delta m_w$ [D 28 equation (9), p 8],

where $\displaystyle \Delta m_w$ is the measured difference in apparent masses.

The air buoyancy correction $\displaystyle C = (\rho_a - \rho_0) \left( \frac{1}{\rho_t} - \frac{1}{\rho_r}\right)$ [D 28 equation (10), p 8] is applied, because the air density differs from $\displaystyle \rho_0$ by more than 10 % [R 111-1 section 10.2.1, p 18].

To determine the uncertainty $\displaystyle u(m_{ct})$ , we’ll need the sensitivity coefficients $\displaystyle \frac{\partial m_{ct}}{\partial m_{cr}} = 1+C \approx 1$ , $\displaystyle \frac{\partial m_{ct}}{\partial C} = m_{cr}$ and $\displaystyle \frac{\partial m_{ct}}{\partial (\Delta m_w)} = 1$ .

Then, $\displaystyle u(m_{ct}) = \sqrt{u(m_{cr})^2 + (m_{cr} \cdot u(C))^2 + u(\Delta m_w)^2}$ , where $\displaystyle u(\Delta m_w)^2 = u_w^2 + u_{ba}^2$ (the uncertainty of the weighing process and the balance, combined) and $\displaystyle m_{cr} \cdot u(C) = u_b$ , in the notation of R 111-1 section C.6, p 66-70.

Expressed as a relative uncertainty, $\displaystyle \frac{u(m_{ct})}{m_{ct}} = \sqrt{\left( \frac{u(m_{cr})}{m_{cr}} \right)^2 + u(C)^2 + \left( \frac{u(\Delta m_w)}{m_{cr}} \right)^2}$ .

From the table above, $\displaystyle \frac{u(m_{cr})}{m_{cr}} = 0.27 \cdot 10^{-6}$ .

From equation (C.6.3-1) of R 111-1 (p 67), $\displaystyle u(C)^2 = \left( \frac{u_b}{m_{cr}} \right)^2$ $\displaystyle = \left( \left( \frac{1}{\rho_t} - \frac{1}{\rho_r}\right) \cdot u(\rho_a) \right)^2 + \left( \frac{(\rho_a - \rho_0)}{\rho_t} \cdot \frac{u(\rho_t)}{\rho_t} \right)^2$ $\displaystyle + \frac{(\rho_a - \rho_0)(\rho_0 + \rho_a - 2 \rho_{al})}{\rho_r^2} \cdot \left( \frac{u(\rho_r)}{\rho_r} \right)^2$ ,

where $\displaystyle \rho_{al}$ is the air density during the last calibration of the reference weight.

Using $\displaystyle \rho_{al} = 1.2 \ \mathrm{kg.m^{-3}}$ , $\displaystyle u(C)^2 = \left( 14 \cdot 10^{-6} \ \mathrm{m^3.kg^{-1}} \cdot 0.005 \ \mathrm{kg.m^{-3}} \right)^2$ $\displaystyle + \left( -39 \cdot 10^{-6} \cdot 0.0088 \right)^2$ + $\displaystyle + \left( -39 \cdot 10^{-6} \cdot 0.0088 \right)^2$ . So, $\displaystyle u(C) = 0.49 \cdot 10^{-6}$ , with the terms in $\displaystyle u(\rho_t)$ and $\displaystyle u(\rho_r)$ dominating over the term in $\displaystyle u(\rho_a)$ .

The term $\displaystyle u( \Delta m_w)$ contains the uncertainty of the weighing process, $\displaystyle u_w$ , which is an ESDM calculated as 0.01 mg, the sensitivity of the balance, $\displaystyle u_s$ , and the display resolution of the balance, $\displaystyle u_d = \frac{0.1 \ \mathrm{mg} /2}{\sqrt{3}} \cdot \sqrt{2} = 0.04 \ \mathrm{mg}$ . (Eccentric loading of the balance is included in $\displaystyle u_w$ , and magnetism is negligible, according to p 69 of R 111-1.) In total, let’s suppose that $\displaystyle u( \Delta m_w) = 0.05 \ \mathrm{mg}$ , so that $\displaystyle \frac{u( \Delta m_w)}{m_{cr}} = 0.05 \cdot 10^{-6}$ .

Finally, $\displaystyle \frac{u(m_{ct})}{m_{ct}} = \sqrt{(0.27 \cdot 10^{-6})^2 + (0.49 \cdot 10^{-6})^2 + (0.05 \cdot 10^{-6})^2} = 0.56 \cdot 10^{-6}$ . So, we have achieved our goal of a relative standard uncertainty smaller than $\displaystyle 0.8 \cdot 10^{-6}$ .

(Contact the author at lmc-solutions.co.za.)

Uncertainty of measurement: emissivity of a reflective foil

August 17, 2014 Hans Liedberg Leave a comment

Reflective foil laminates are used in thermal insulation of buildings. A standard test method [SANS 1381-4] describes the measurement (amongst other properties) of their emissivity using a thermopile radiation thermometer. This article describes how to estimate the uncertainty of measurement (UoM) in this application of infrared radiation thermometry.

The documentary standard SANS 1381-4 requires that the emissivity of one reflective surface of the specimen being tested be less than or equal to 0.05, or 5% (clause 4.8).
To measure the emissivity (clause 5.8), half of the specimen’s surface is painted black, the specimen is heated to 70 °C (presumably, this temperature is chosen to represent a typical situation in use, in a ceiling or around a hot water geyser), and the total amounts of thermal radiation coming from the reflective part and from the blackened part are measured by a calibrated thermopile (clause 5.8.1.2). The emissivity of the blackened part, $\displaystyle \varepsilon_b$ , is assumed to be 0.95, or 95% (clause 5.8.1.3). The thermopile output signals when viewing the reflective part, $\displaystyle E_1$ , and the blackened part, $\displaystyle E_0$ , are used to calculate the emissivity of the reflective part, $\displaystyle \varepsilon$ , as follows: $\displaystyle \frac{\varepsilon}{\varepsilon_b} \approx \frac{E_1}{E_0}$ , or $\displaystyle \varepsilon \approx \frac{E_1}{E_0} \varepsilon_b$ (clause 5.8.4).

To understand the relationship between thermopile output, target emissivity and temperature, let’s analyse the heat transfer to and from the detector surface (thermopile hot junction):

Let the target (foil) temperature be $\displaystyle T$ (70 °C, in this case), ambient temperature be $\displaystyle T_a$ (probably 23 °C), thermopile hot junction temperature be $\displaystyle T_h$ and thermopile cold junction temperature be $\displaystyle T_c$ .

The voltage output of the thermopile, $\displaystyle E$ , is proportional to the difference between hot and cold junction temperatures, that is, $\displaystyle E = S(T_h-T_c)$ .

We express the total amounts of thermal radiation using the Stefan-Boltzmann law. The nett thermal radiation entering the detector is the sum of that emitted by the target to the thermopile hot junction, $\displaystyle \varepsilon \sigma T^4$ , plus that reflected by the target from the surroundings to the hot junction, $\displaystyle (1 - \varepsilon) \sigma {T_a}^4$ , minus that emitted from the hot junction, $\displaystyle \sigma {T_h}^4$ .

Heat transferred by convection from the thermopile hot junction to the adjacent air is $\displaystyle hA(T_h-T_a)$ , where $\displaystyle h$ is the convection heat transfer coefficient and $\displaystyle A$ is the surface area of the hot junction or detector.

This is all the heat transferred from the outside world to the detector surface (hot junction). At equilibrium, it is balanced by heat transferred from the hot junction towards the cold junction (within the body of the detector) by conduction. This heat flow causes a temperature gradient between hot and cold junctions, with the thermal conductivity of the detector body, $\displaystyle k$ , relating the temperature difference to the amount of heat flowing: $\displaystyle \frac{kA}{L}(T_h-T_c)$ , where $\displaystyle L$ is the distance between hot and cold junctions.

At equilibrium, the heat transferred to the detector surface by radiation and convection should be equal to that lost to the cold junction side by conduction: $\displaystyle \varepsilon \sigma T^4 + (1 - \varepsilon ) \sigma {T_a}^4 - \sigma {T_h}^4 - hA(T_h-T_a) = \frac{kA}{L}(T_h-T_c)$ .

Rearranging the above equation, $\displaystyle \sigma ({T_h}^4 - {T_a}^4) + (\frac{k}{L}+h)AT_h - \frac{k}{L}AT_c - hAT_a = \varepsilon \sigma (T^4 - {T_a}^4)$ .

Let us assume that the thermopile backside has an efficient heatsink, so that $\displaystyle T_c \approx T_a$ . (Deviations from ideal behaviour, for example, due to changes in the thermopile cold junction temperature with increasing incident radiation, should be evident from the thermopile’s calibration results.) Then, the equation becomes $\displaystyle \sigma ({T_h}^4 - {T_a}^4) + (\frac{k}{L}+h)A(T_h - T_a) \approx \varepsilon \sigma (T^4 - {T_a}^4)$ .

At this point, I get stuck: I would hope to reduce this to $\displaystyle K(T_h-T_a) \approx \varepsilon (T^4 - {T_a}^4)$ or, equivalently, $\displaystyle K(T_h-T_c) \approx \varepsilon (T^4 - {T_a}^4)$ , so that thermopile output $\displaystyle E$ is proportional to $\displaystyle \varepsilon (T^4 - {T_a}^4)$ .

Returning to the simple equation $\displaystyle \varepsilon \approx \frac{E_1}{E_0} \varepsilon_b$ used in SANS 1381-4, let’s identify the sources of uncertainty:

The dependence of the thermopile output $\displaystyle E$ on target temperature $\displaystyle T$ and ambient temperature $\displaystyle T_a$ is shown on the right-hand side of the equation derived above. As $\displaystyle E_1$ and $\displaystyle E_0$ are functions of $\displaystyle T$ and $\displaystyle T_a$ , any variation in these temperatures will cause variation in the signals $\displaystyle E_1$ and $\displaystyle E_0$ . The ratio $\displaystyle \frac{E_1}{E_0}$ does not depend on the values of $\displaystyle T$ and $\displaystyle T_a$ , as these terms are the same in numerator and denominator and cancel out, but only on their stability during the time required to measure $\displaystyle E_1$ and $\displaystyle E_0$ . For this reason, we do not explicitly include uncertainties in these temperatures, but rely on them being captured in the standard deviations of $\displaystyle E_1$ and $\displaystyle E_0$ .

The uncertainty in thermopile output signals introduced by the digital multimeter (DMM) used to measure them is typically around $\displaystyle 50*10^{-6}$ of the measured signal (for a 6.5-digit DMM). This is negligible, compared to the repeatability components (experimental standard deviation of the mean, or ESDM) and uncertainty in the emissivity of the blackened part of the specimen. For this reason, we do not consider uncertainties arising from the DMM any further.

The distance between the thermopile detector and the target (reflective part or blackened part of the specimen) should not affect the results, provided that the target always fills the field-of-view of the detector. So, as long as the detector is close enough to the specimen, no uncertainty results from slight variation in this distance.

The standard deviations (ESDM, to be precise) of $\displaystyle E_1$ and $\displaystyle E_0$ must be taken into account. As $\displaystyle E_1$ is typically a very small value, its ESDM is particularly significant (see numerical example, below).

The relative uncertainty in $\displaystyle \varepsilon_b$ is roughly estimated to be $\displaystyle \frac{u(\varepsilon_b)}{\varepsilon_b} = 0.05$ . (In other words, $\displaystyle \varepsilon_b = 95 \% \pm 5 \%$ .) If this component appears to be significant in the following numerical example, we will try to estimate it more precisely.

Numerical example:

Measurements of $\displaystyle E_1$ : 1 μV, 8 μV, 0 μV, 11 μV, 6 μV and 9 μV. (Mean = $\displaystyle 5.8 \rm{\mu V}$ , standard deviation = $\displaystyle 4.4 \rm{\mu V}$ , ESDM = $\displaystyle \frac{4.4 \rm{\mu V}}{\sqrt{6}} = 1.8 \rm{\mu V}$ , relative uncertainty $\displaystyle \frac{u(E_1)}{E_1} = \frac{1.8 \rm{\mu V}}{5.8 \rm{\mu V}} = 0.3$ .)

Measurements of $\displaystyle E_0$ : 424 μV, 411 μV, 410 μV, 417 μV, 378 μV and 378 μV. (Mean = $\displaystyle 403 \rm{\mu V}$ , standard deviation = $\displaystyle 20 \rm{\mu V}$ , ESDM = $\displaystyle \frac{20 \rm{\mu V}}{\sqrt{6}} = 8.2 \rm{\mu V}$ , relative uncertainty $\displaystyle \frac{u(E_0)}{E_0} = \frac{8.2 \rm{\mu V}}{403 \rm{\mu V}} = 0.02$ .)

Result for emissivity: $\displaystyle \varepsilon \approx \frac{E_1}{E_0} \varepsilon_b = \frac{5.8 \rm{\mu V}}{403 \rm{\mu V}} * 0.95 = 0.014$ , or 1.4%.

As the relation between $\displaystyle \varepsilon$ and $\displaystyle E_1$ , $\displaystyle E_0$ and $\displaystyle \varepsilon_b$ is one of simple multiplication and division, we can combine the relative uncertainties simply:

$\displaystyle \frac{u(\varepsilon)}{\varepsilon} = \sqrt{\left( \frac{u(E_1)}{E_1} \right)^2 + \left( \frac{u(E_0)}{E_0} \right)^2 + \left( \frac{u(\varepsilon_b)}{\varepsilon_b} \right)^2} = \sqrt{0.3^2 + 0.02^2 + 0.05^2}$ .

The effective degrees of freedom, $\displaystyle \nu_{eff}$ , will be close to those of the dominant component, $\displaystyle u(E_1)$ : $\displaystyle \nu_{E_1} = n-1 = 5$ , since $\displaystyle n=6$ readings were taken. For $\displaystyle \nu_{eff} = 5$ , the coverage factor for a level of confidence of 95.45% is 2.65. So, the expanded relative uncertainty is $\displaystyle \frac{U(\varepsilon)}{\varepsilon} = 2.65 * 0.3 = 0.8$ , the expanded absolute uncertainty is $\displaystyle U(\varepsilon) = 0.8 * 0.014 = 0.011$ and the measurement result is $\displaystyle \varepsilon = 0.014 \pm 0.011$ , or $\displaystyle \varepsilon = 1.4 \% \pm 1.1 \%$ .

Take care! When the quantity being measured (emissivity, in this case) is dimensionless and expressed in percent, and its relative uncertainty is expressed in percent, confusion can arise. The expanded relative uncertainty estimated above is 0.8, or 80%, of the measured value. It is not already an absolute uncertainty in emissivity, in other words, the result is not $\displaystyle \varepsilon = 1.4 \% \pm 80 \%$ , which would be nonsensical.

We see that $\displaystyle \frac{u(E_1)}{E_1}$ is the dominant component of uncertainty, by far. As $\displaystyle \frac{u(\varepsilon_b)}{\varepsilon_b}$ is unlikely to be significant compared to this, it is not necessary to estimate the latter component more precisely than the rough estimate we used earlier.

Note, regarding the simple combination of relative uncertainties performed above: This is only correct when the function is one of simple multiplication and division. For more general situations, the sensitivity coefficient must be determined by taking the partial derivative. The equivalence of these approaches for the simple equation $\displaystyle \varepsilon \approx \frac{E_1}{E_0} \varepsilon_b$ is demonstrated below:

$\displaystyle u(\varepsilon) = \sqrt{\left( \frac{\partial \varepsilon}{\partial E_1} u(E_1) \right)^2 + \left( \frac{\partial \varepsilon}{\partial E_0} u(E_0) \right)^2 + \left( \frac{\partial \varepsilon}{\partial \varepsilon_b} u(\varepsilon_b) \right)^2} = \sqrt{\left( \frac{\varepsilon_b}{E_0} u(E_1) \right)^2 + \left( \frac{-E_1 \varepsilon_b}{{E_0}^2} u(E_0) \right)^2 + \left( \frac{E_1}{E_0} u(\varepsilon_b) \right)^2}$ $\displaystyle = \sqrt{\left( \frac{\varepsilon}{E_1} u(E_1) \right)^2 + \left( \frac{-\varepsilon}{E_0} u(E_0) \right)^2 + \left( \frac{\varepsilon}{\varepsilon_b} u(\varepsilon_b) \right)^2} = \varepsilon \sqrt{\left( \frac{u(E_1)}{E_1} \right)^2 + \left( \frac{-u(E_0)}{E_0} \right)^2 + \left( \frac{u(\varepsilon_b)}{\varepsilon_b} \right)^2}$ .

(Contact the author at lmc-solutions.co.za.)

Preparation and use of the ice point in Thermometry

June 19, 2014 Hans Liedberg 1 Comment

For a Temperature calibration laboratory, a testing laboratory or any other business that needs to verify the accuracy of its thermometers, the ability to realise the ice point is perhaps the most important and most basic of Thermometry capabilities.

Q: What are some of the uses of the ice point?

A: 1. Intermediate checks of resistance thermometers (PRTs and thermistors) and liquid-in-glass thermometers:

Some method of verifying the accuracy of measuring equipment between calibrations is usually required by a quality management system, so that the equipment’s reliability can be checked when necessary, preferably without the inconvenience of using an external calibration service. It is possible to compare a thermometer to another of similar or greater accuracy, but using an “absolute” measurement standard like the ice point is often more convenient. (The ice point can be realised to an accuracy of about ± 0.01 °C without too much trouble.)

Note: Measurement at the ice point is not a very sensitive in-service check for thermocouples. For a PRT, a change from 100.0 Ω to 100.1 Ω (0.25 °C) at 0 °C is equivalent to a change from 300.0 Ω to 300.3 Ω (0.75 °C) at 550 °C, but, for a type K thermocouple, a 10 µV (0.25 °C) change at 0 °C is equivalent to a 260 µV (7 °C) change at 550 °C. This makes it necessary to check thermocouples at a temperature further from ambient (for example, at 200 °C) to draw meaningful conclusions about drift.

2. Recalibration of liquid-in-glass (LIG) thermometers:

If a LIG thermometer is not used above 200 °C or so, all significant changes in calibration will be due to changes in bulb volume, not to changes in the capillary [Cross et al, Maintenance, Validation, and Recalibration of Liquid-in-Glass Thermometers, NIST SP 1088, 2009]. (We do not consider gross errors, such as a separated liquid column, here.) The effect of such changes in the bulb (for example, secular change and temporary depression of zero) may be evaluated by observing the temperature indicated by the thermometer at the ice point. (Comparison with a calibrated reference thermometer of equal or greater accuracy, in a uniform-temperature environment, is also an option, but the ice point is often simpler.) Past calibration results for the thermometer may then be adjusted by a constant offset, to compensate for the difference between the present and past indicated temperatures at 0 °C. (For example, if the reading at 0 °C rises from -0.4 °C to -0.3 °C, the reading at 100 °C will also rise by 0.1 °C.) This single-point recalibration technique, combined with regular visual inspection to identify problems such as a separated liquid column, is often sufficient to assure the quality of measurement results, avoiding the need for expensive and time-consuming recalibration at an external calibration laboratory.

(Note: We must evaluate how well we can realise and use an ice point, before relying on it unreservedly. To do so, measure a thermometer at the ice point yourself, immediately before and/or after it returns from calibration, and compare your result(s) to that reported in the calibration certificate. Repeat this check periodically, to evaluate reproducibility. Bear in mind the uncertainty of calibration and the accuracy to which you can read the thermometer, when interpreting the results.)

3. Calibration or intermediate checks of low-temperature infrared radiation thermometers:

The emissivities of ice and liquid water at infrared wavelengths longer than 2 µm are high (~0.96), making it easy to create a blackbody target (emissivity ≈ 1) for calibration of low-temperature infrared radiation thermometers. (Such thermometers usually operate in the wavelength range 8 to 14 µm.)

Note: When aiming the thermometer at the ice point, take care to view an area of melting ice. The top surface of the ice may often not contain liquid water, and may be at a temperature colder than 0 °C: rather make a hole in the ice and view an area of grey slush, lower down. The hole also increases the effective emissivity of the target.

4. For a reference PRT in a calibration laboratory, adjustment of its calibration results to compensate for drift:

If a PRT is bumped and its resistance increases, the relative change in resistance is usually similar over the whole temperature range. For example, a change from 100.0 Ω to 100.1 Ω at 0 °C (a 0.1 % increase) will usually mean a change from 300.0 Ω to 300.3 Ω at 550 °C (again, a 0.1 % increase). If the calibration certificate reports a curve of resistance as a function of temperature, it will usually be written in terms of a resistance ratio, R(T)/R(0.01 °C) or R(T)/R(0.00 °C). If the user can measure R(0.00 °C) sufficiently accurately, he may use his latest measurement at the ice point to calculate the resistance ratio, thereby compensating for much of the drift in R(T) since the PRT’s calibration.

Notes:

(i) To calculate R(0.01 °C) from the measured resistance at the ice point, R(0.00 °C), use R(0.01 °C) = R(0.00 °C) / W(0.00 °C) = R(0.00 °C) / 0.99996.

(ii) If the user uses his own measurement of R(0 °C) in the calculation of resistance ratio (and, subsequently, temperature), he must include the uncertainty of that measurement in the uncertainty of the calculated temperature. For this reason, it is only sensible to use your own measurement of R(0 °C) to compensate for drift, if the uncertainty in that value is smaller than the typical drift for which you are trying to compensate.

5. For a reference PRT measured on an ohmmeter or a resistance bridge, elimination of most resistance measurement errors:

If the PRT’s calibration results are expressed in terms of resistance ratio (as discussed above), the user can eliminate the effect of most errors in resistance measurement, by measuring both R(T) and R(0 °C) on the same range of the same measuring instrument. Then, the resistance ratio will be independent of any linear errors in the resistance measuring instrument, including, most importantly, any drift in a reference resistor or reference voltage since its last calibration. The only resistance measurement errors that still have an effect are those that are not proportional to the measured resistance value.

6. For a thermocouple, more accurate cold junction temperature:

The output of a thermocouple depends on the temperature difference between the measuring (or “hot”) junction and the reference (or “cold”) junction: any uncertainty in the reference junction temperature causes an uncertainty in the calculated temperature of the measuring junction. While electronic Cold Junction Compensation typically measures the temperature of the reference junction to an accuracy of ± (0.5 to 0.1) °C, immersing the reference junction in an ice point controls its temperature to 0.00 °C ± 0.01 °C, that is, an order of magnitude more accurately.

Q: How do we prepare an ice point?

A: The container in which the ice point is to be prepared should be thermally insulated. A wide-mouthed vacuum flask, 80 mm to 100 mm in diameter and 200 mm to 400 mm deep, is ideal. For convenience in cleaning the flask and packing the ice, it should not have a narrow neck. (It is convenient if you can fit your hand inside it.) If the thermal insulation at the bottom of the flask is good enough, a thermometer can be inserted all the way to the bottom without the tip being in a hot spot. (Vacuum insulation is better than expanded polystyrene.)

The ice to be used must be crushed or shaved, preferably to a chip size of 1 mm or less. It is preferable, but not essential, to make it from distilled or deionised water.

Sufficient liquid water should be available to fill approximately one third of the thermally insulated container. Again, distilled or deionised water is preferred, but tap water may be used.

A scoop will assist in handling the ice without contaminating it with salts from the hands.

Scoop the crushed ice into the container, adding liquid water until the ice appears translucent or grey. (This indicates that it is melting, and therefore at 0 °C. White, frosty ice is usually colder than 0 °C.) Compact the ice, so that it is packed against the bottom of the container and is not floating on top of liquid water.

Insert the first thermometer to be measured, to the appropriate depth, wait 3 to 20 minutes for thermal equilibrium (five minutes is usually sufficient) and record its reading. When first realising the ice point, and periodically (perhaps monthly) thereafter, this thermometer should be one that has been calibrated to a high accuracy at 0 °C, to provide data on the deviation of your ice points from the desired temperature of 0.00 °C, and their stability in temperature.

Insert the next thermometer to be measured, ensuring that it is in good contact with the ice (particularly if you insert it in a previously used hole).

Drain off excess water when necessary, and re-compact the ice. (To determine how long it takes for an excess of liquid water to accumulate, insert a high-resolution thermometer to the bottom of an ice point and record its readings regularly over several hours, noting when they start to rise.)

(Contact the author at lmc-solutions.co.za.)

Metrology Rules

Category Archives: Articles

Conformity to specification – calculating risk and implementing a decision rule in Excel or Calc

Comparing temperature sensors in an unstable environment: the effect of response time

Uncertainty of measurement: pressure dead-weight tester

Control of measuring equipment – the requirements of ISO 9001

Uncertainty of measurement: water vapour transmission of materials

Calibrating a platinum resistance thermometer at a fixed point

Uncertainty of measurement: relative humidity via dew point and air temperature

Uncertainty of measurement: conventional mass of a weight

Uncertainty of measurement: emissivity of a reflective foil

Preparation and use of the ice point in Thermometry

For Metrologists by Metrologists